Attention Is All You Need 链接到标题

* Authors: [[Ashish Vaswani]], [[Noam Shazeer]], [[Niki Parmar]], [[Jakob Uszkoreit]], [[Llion Jones]], [[Aidan N. Gomez]], [[Lukasz Kaiser]], [[Illia Polosukhin]]

• Local library

初读印象 链接到标题

transformer 是第一个完全由 attention 构成的时序模型。相比于传统基于 RNN 和 CNN 的模型， 它在精度、并行度和长距离依赖上带来了明显提升。

文章骨架 链接到标题

%%创新点到底是什么?%% novelty:: 第一个完全由 attention 构成的时序模型

%%有什么意义？%% significance:: 适用于并行化计算，和它本身模型的复杂程度导致它在精度和性能上都要高于之前流行的RNN循环神经网络。

%%有什么潜力?%% potential:: 目前 transformer 已经成为在 nlp、 cv 、多模态领域最常用的基础结构

TL;DR 链接到标题

Attention is all you need 是第一个完全由 attention 构成的时序模型。相比于传统基于 RNN 和 CNN 的模型， 它在精度、并行度和长距离依赖上带来了明显提升。

论文本身忽略了很多细节， 读起来不是很好懂， 推荐同时阅读 Jay Alammar 的博客 The Illustrated Transformer 帮助理解。

Dataset/Algorithm/Model/Experiment Detail 链接到标题

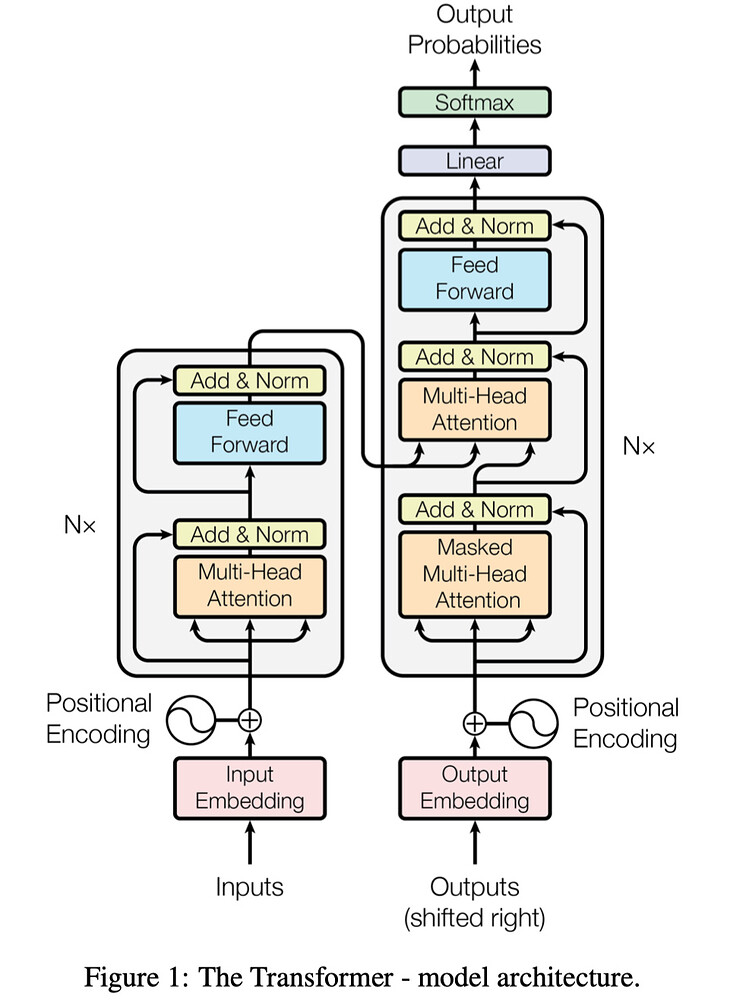
模型的整体结构如下图所示：

从整体上看， Transformer 由 Encoder 和 Decoder 两大部分组成，Encoder 部分由若干个 [Multi-Head Attention + Feed-Forward] 堆叠而成，Decoder 由若干个 [Masked Multi-Head Attention + Multi-Head Attention] 组成，Encoder 的输入（图中 “Inputs”）为待翻译的文本（例如德文转英文任务中它是待翻译的德文），而 Decoder 部分的输入（图中 “Outputs”）为已经翻译的文本（例如德文转英文任务中已经转好的英文） ， 每个 Multi-Head Attention layer 有 3 个输入（Q、K 和 V 具体含义后面介绍），需要注意的是 Decoder 中间的 Multi-Head 的输入的 K 和 V 来自于 Encoder 的最后一个 sublayer 的输出， Q 来自于前一个模块的输出。下面详细讲解其中的 Attention 原理。

Transformer 里的 Attention 机制 链接到标题

Multi-Head Attention 内部结构如下图所示， 首先我们介绍其中最重要的 Scaled Dot-Product Attention 结构。

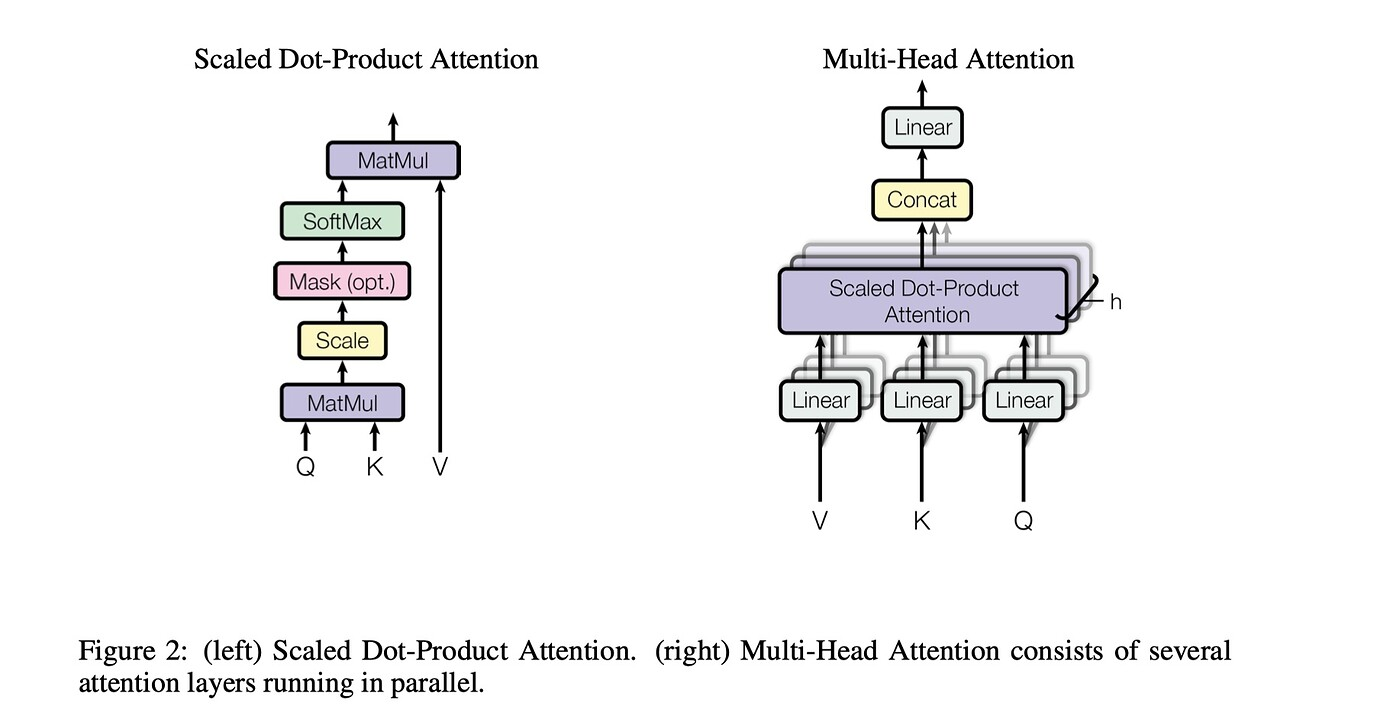
Scaled Dot-Product Attention 链接到标题

$ \operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V $

我们可以看到，这个结构有 3 个输入向量 Q(Query)、K(Key)、V(Value)，他们是用 embedding 向量和三个随机初始化的权重矩阵 $W^Q$ 、 $W^K$ 、 $W^V$ 相乘的结果。这三个向量的作用是什么呢？想象我们在图书馆里找一本C++的入门书，这个查询词“一本C++ 的入门书”就是Q，图书馆里会把书籍分门别类比如“哲学”、“技术”、“人文”，这相当于K，而图书馆里的书就是 V。

得到三个输入向量后，首先将 $Q$ 和 $K$ 做 matmul 后输入 softmax 得到 query 和每个 key 的匹配权重，这个匹配权重就是我们说的 attention， 然后将这个权重作用于 V 上就能知道当前的输入和哪个输入最相关，最后将分配加权后的 V 求和就得到了最终输出结果。回到上面的例子， 第一个 matmul 的过程相当于我们根据查询词和图书馆的分类系统做匹配，根据匹配程度，我们知道 “C++入门书” 应该和 “技术” 这个书类最为接近， 因此， 我们应该把注意力集中到这个书类的书上面（第二个matmul）。引用博客中的一张图可以看得更加明显一些：

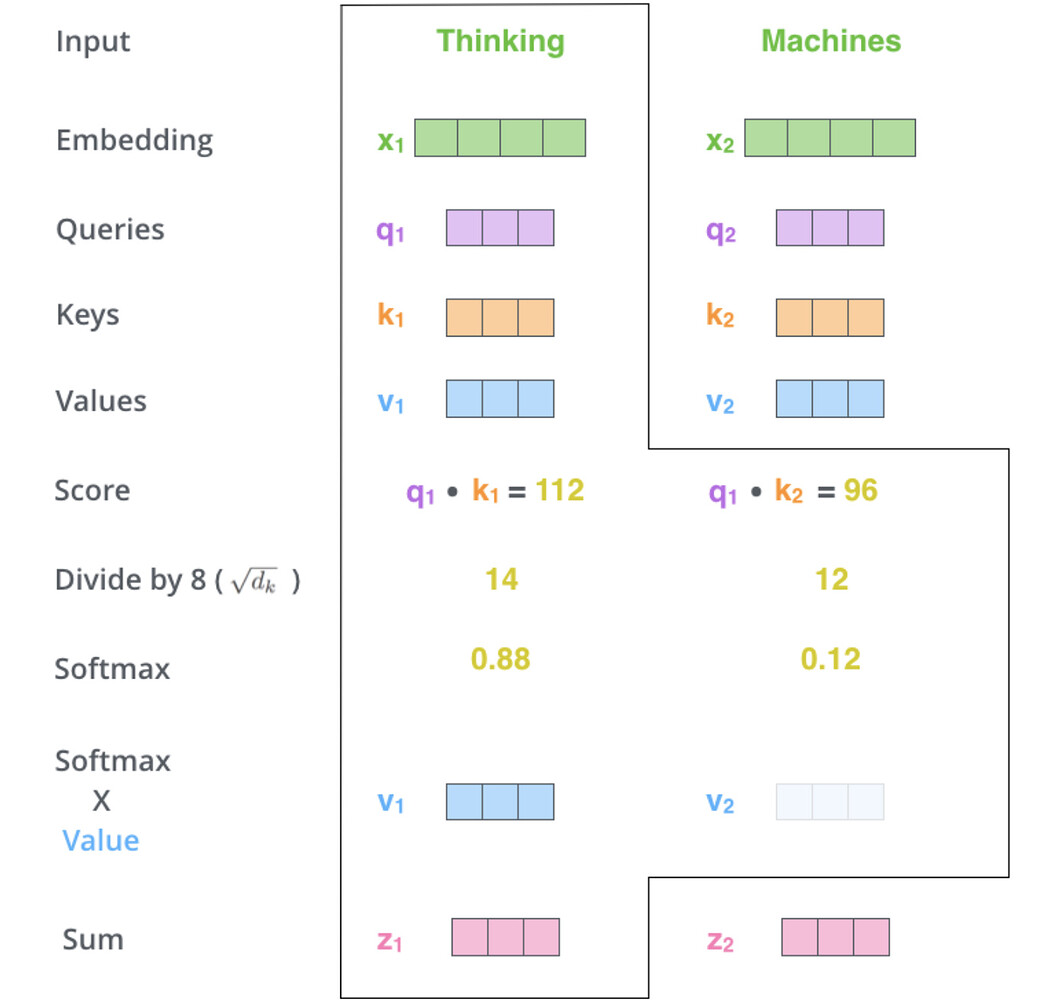
需要注意的是， 我们上面的公式中，对矩阵乘的结果除以了一个 $\sqrt{d_k}$ , 其中 $d_k$ 是 query 向量和 key 向量的维度， 它的作用是防止当输入维度很长时，导致乘积结果太大而进入 softmax 饱和区， 影响梯度传播。

从矩阵角度来看的话它的过程如图：

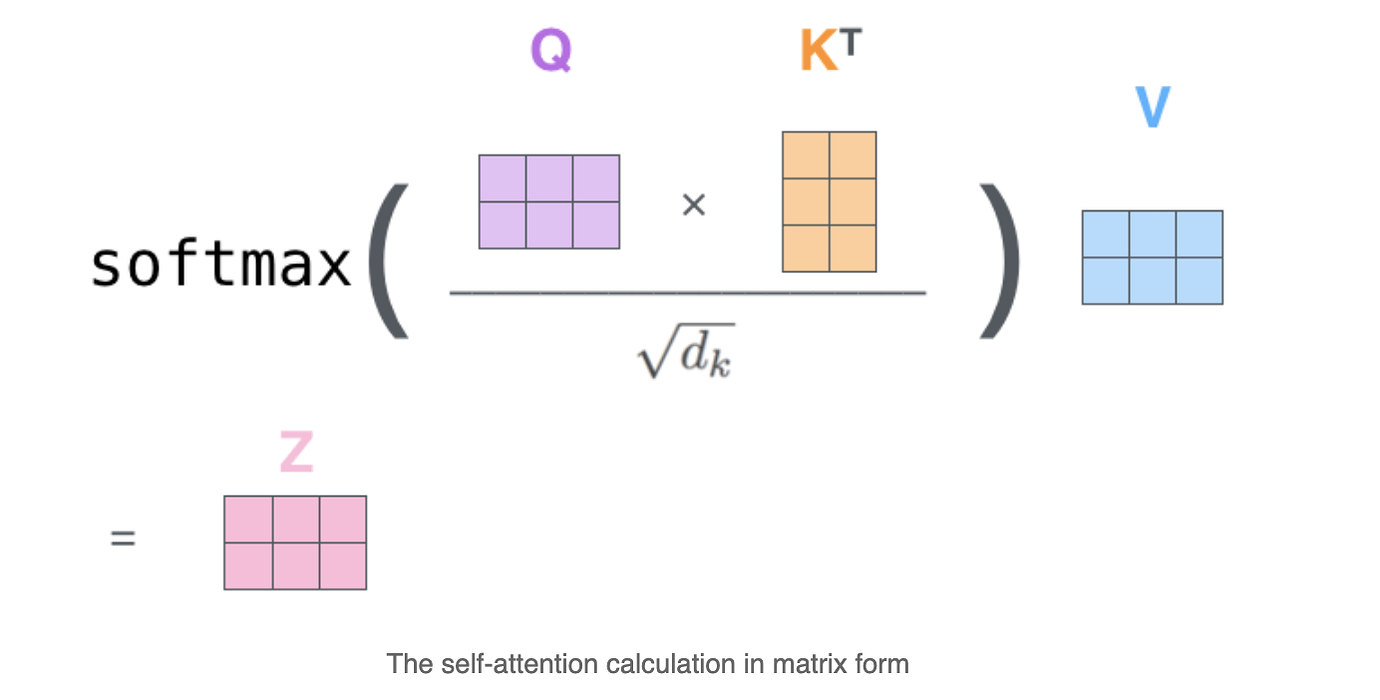
Multi-Head Attention 链接到标题

Multi-Head Attention 是对上面的 attention 机制的加强，上面只使用了一个随机初始化的权重来将 embedding 映射到 Q、K、V， 如果我们将映射矩阵扩展到 h 个， 即 $W_0^Q, W_1^Q … W_h^Q$ 、 $W_0^K、W_1^K…W_h^K$ 、 $W_0^V、 W_1^V … W_h^V$ 于 embedding matmul 之后得到 h 种输入， 分别送入上面的 Scaled Dot-Product Attention 结构里就可以获得 h 个不同的加权结果 $z_0,z_1…z_h$ ， 之后将他们concat 在一起后过一个 $W^O$ 降维。

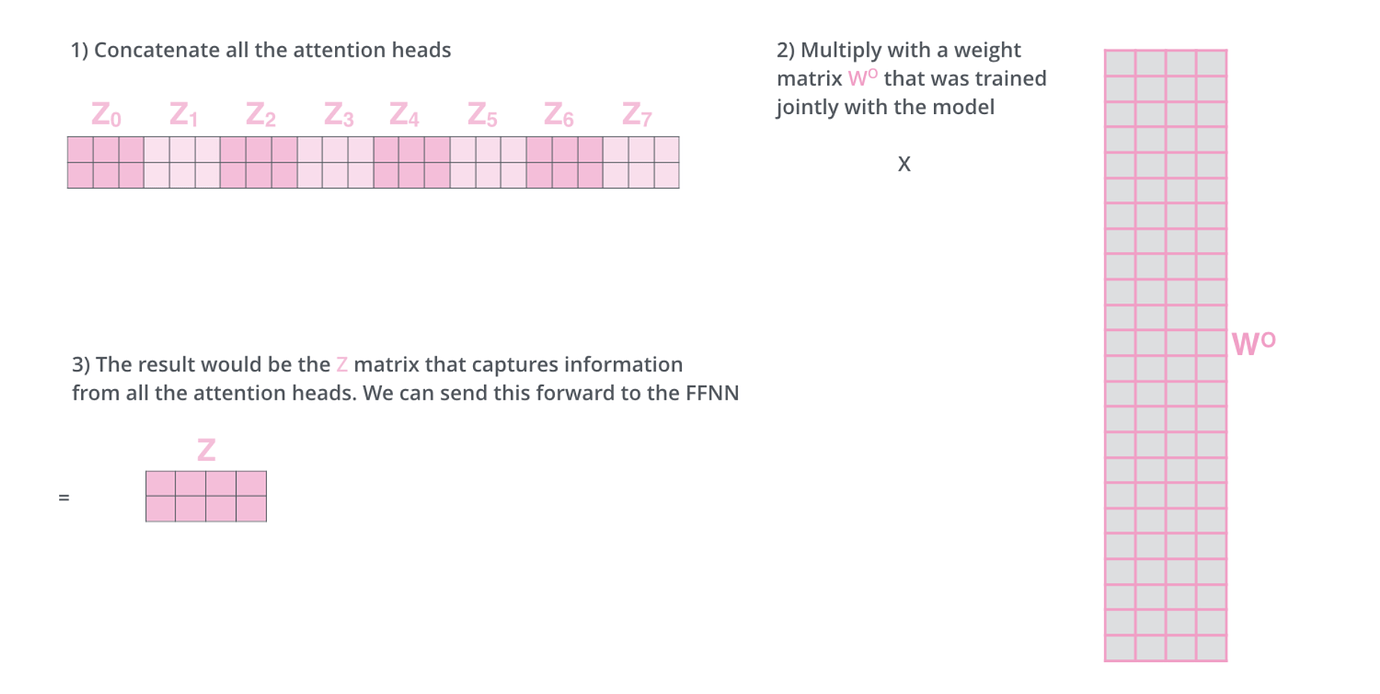
公式如下：

$\begin{aligned} \operatorname{MultiHead}(Q, K, V) &=\text { Concat }\left(\operatorname{head} {1}, \ldots, \text { head } {\mathrm{h}}\right) W^{O} \ \text { where head } {\mathrm{i}} &=\operatorname{Attention}\left(Q W {i}^{Q}, K W_{i}^{K}, V W_{i}^{V}\right) \end{aligned}$

这么做的好处是

1. 让模型关注更多样化的区域：由于不同矩阵初始化值不同，能够使得模型关注更加多样化的区域。
2. 增加表达子空间，由于初始化的不同， 可以将输入映射到不同的子空间，增加模型的表达能力。

位置编码 链接到标题

到目前为止，这个模型还没有能够区分输入顺序的能力，也就是说，我们把一句话的单词任意打乱位置，得到的结果是一样的，作者引入了位置编码来解决这个问题。

位置编码的原理是对于每个输入位置分配一个唯一的编码，并将它附加在原始输入上，这样输入除了原本的信息之外就带上了位置信息。下面是一个简单的例子。

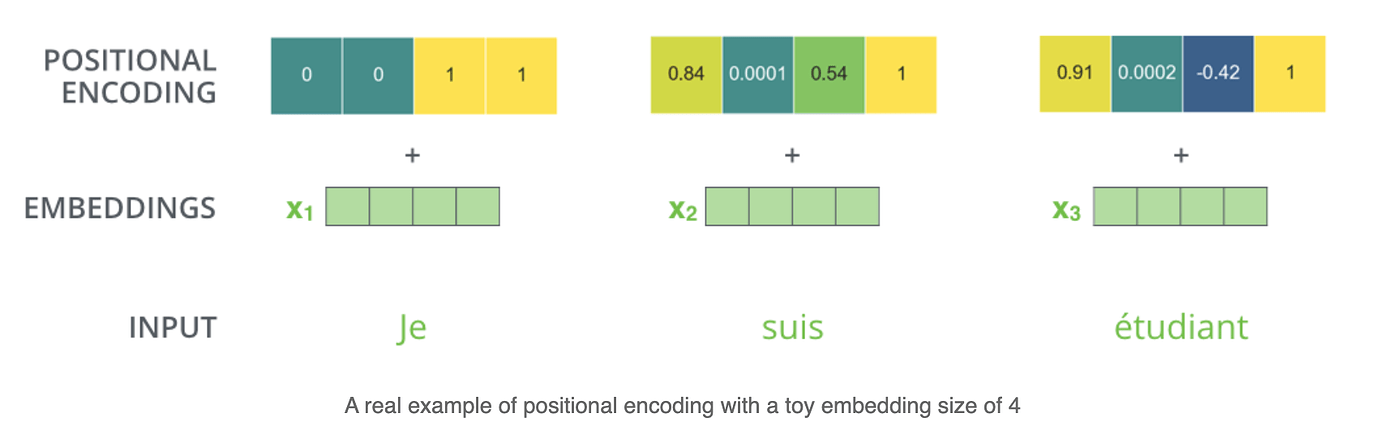
文中，作者采用了三角函数形式的位置编码：

$\begin{aligned} P E_{(p o s, 2 i)} &=\sin \left(p o s / 10000^{2 i / d_{\mathrm{model}}}\right) \ P E_{(p o s, 2 i+1)} &=\cos \left(p o s / 10000^{2 i / d_{\mathrm{model}}}\right) \end{aligned}$

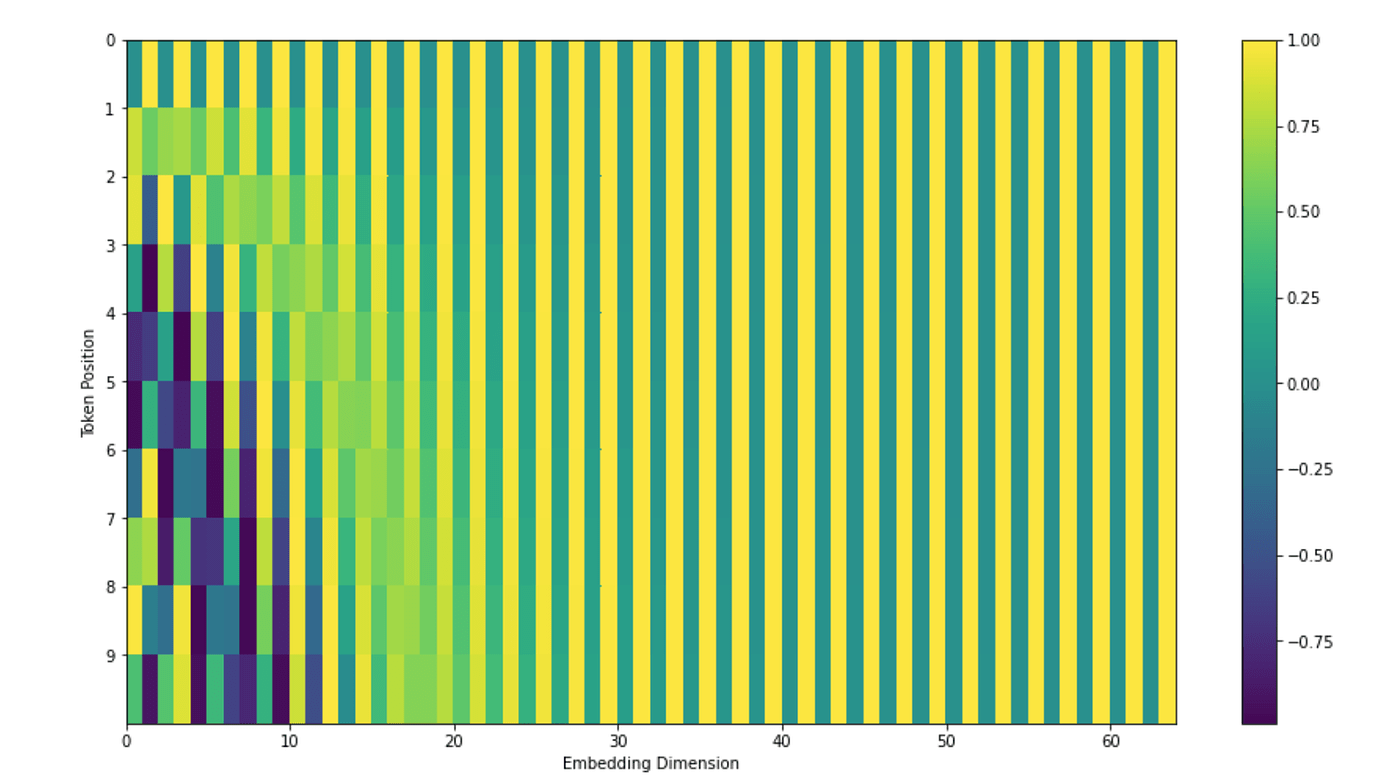
其中 pos 为单词在句子中的位置， 而 i 表示编码的 dimension，采用三角函数的原因是它能用和差公式将不同位置的编码表示成线性关系并且对于在测试中遇到了长度大于训练最大长度的句子，这个编码仍然能够起作用（三角函数周期性）。另外可以看到，编码的偶数 dimension 位置采用 sin 函数，奇数位置采用的是 cos 函数， 它的图像如下所示：

Thoughts 链接到标题

1. Transformer 将时序模型中的 CNN RNN 结构抛弃带来了高精度、高并行化、和将长距离依赖缩小的到 1 的好处
2. 高精度：使用 6 层 Encoder + 6 层 Decoder 的结果，取得了 English2German English2French 机器翻译 BLEU 最高性能。
3. 高并行化：Encoder 部分不依赖于时序， 可以快速的并行计算， Decoder 部分的输入依赖之前时刻的输出，貌似并行不起来， 猜测训练的时候可以通过 mask 把一些依赖给关掉？这一点还没有完全理解
4. 减少长距离依赖：在 Encoder 部分，单个 q 会同时和 所有的 k 计算 attention， 计算过程和单词之间的实际距离没有关系。
5. Transformer 为 DL 领域带来了新的思路，涌现出了 ViT 等优秀工作，在 CV 等领域 “出圈”，成为一个研究热点。
6. 为了处理长距离依赖关系，而丢失了局部信息捕捉能力