Swin Transformer: Hierarchical Vision Transformer using Shifted Windows 链接到标题
* Authors: [[Ze Liu]], [[Yutong Lin]], [[Yue Cao]], [[Han Hu]], [[Yixuan Wei]], [[Zheng Zhang]], [[Stephen Lin]], [[Baining Guo]]
初读印象 链接到标题
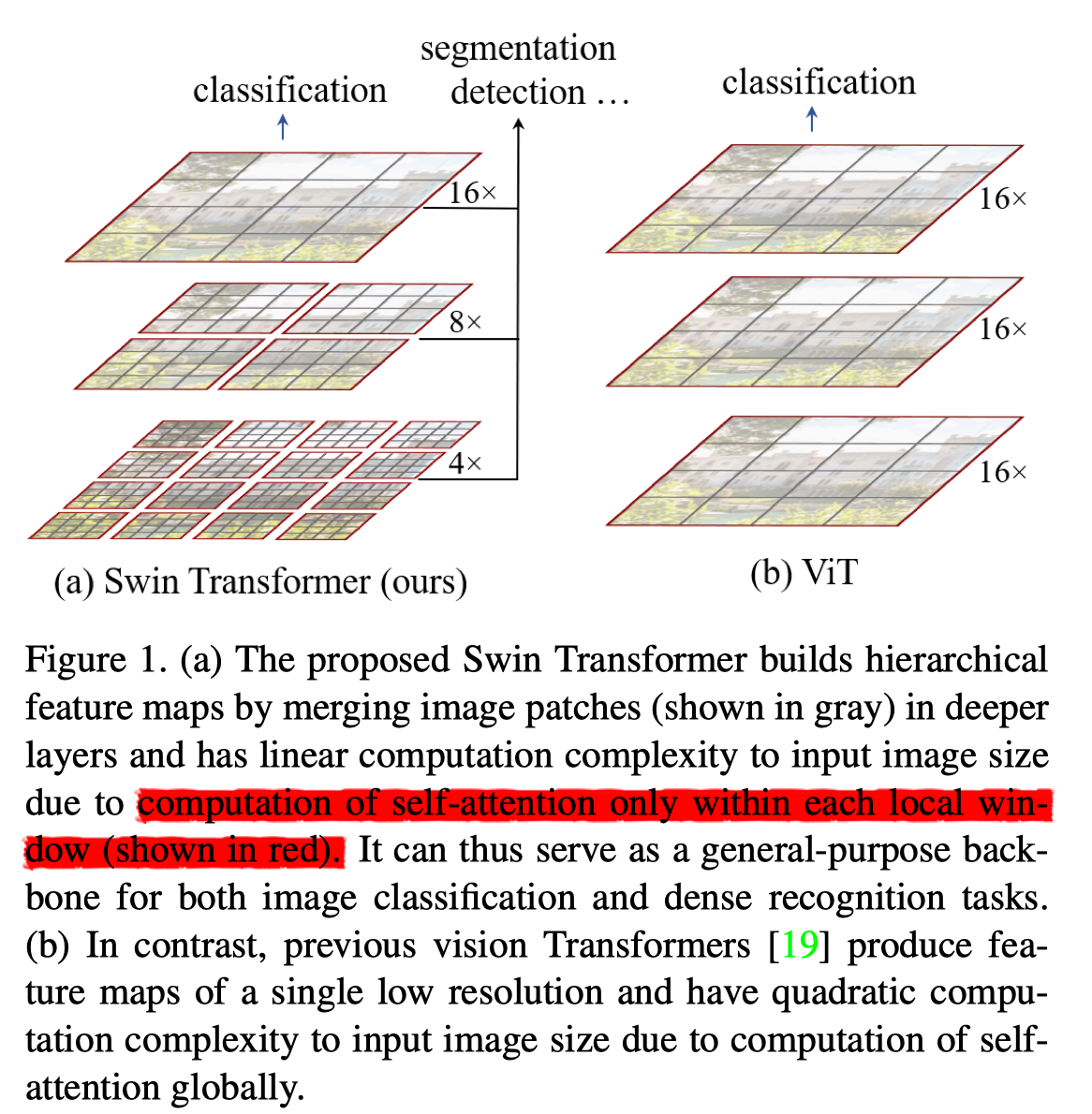
提出了一种包含滑窗操作,具有层级设计的Swin Transformer, 一方面能引入CNN卷积操作的局部性,另一方面能节省计算量。
文章骨架 链接到标题
%%创新点到底是什么?%% novelty:: 提出了一种包含滑窗操作,具有层级设计的Swin Transformer
%%有什么意义?%% significance:: 一方面能引入CNN卷积操作的局部性,另一方面能节省计算量
%%有什么潜力?%% potential:: 在多项视觉任务上取得了SOTA的结果, 比如分类(ImageNet-1K 上 top-1 acc 87.3),检测(COCO 58.7 box AP 提升 2.7, 51.1 mask AP 提升 2.6),分割(ADE20K 53.5 mIoU 提升 3.2)
TL;DR 链接到标题
问题: 当前 ViT 计算复杂度太高的问题,原因cv相对于 nlp 数据规模大、复杂度和 HW 成平方关系 方法:hierarchical Transformer + shifted windows 贡献:
- 复杂度由 $O((WH)^2)$ 减少到 $O(WH)$;
- 一个可以同时在 classification、 detection、 segmentation 等任务上使用的基础 ViT backbone;
- 在 ImageNet、COCO 检测/分割 上达到 SOTA
Method 链接到标题

如上图所示, Swin Transformer 采用层次结构,每层划分不重叠的 windows, 然后在每个windows内和 ViT 类似切patch,提 feature, 随着层次加深,合并前层的相邻 patchs, 由于每层划分的窗口是固定的,所以整体时间复杂度和 $(HW)$ 成线性关系。
因为窗口是无重叠划分的,窗口之间缺乏信息交流,作者提出一种 shifted windows 用于将前一层的窗口之间的信息做联通。
如下图所示:第 l 层使用普通的窗口切分方法,第 l+1 层对窗口向x和y方向上同时做了偏移,这样 l + 1 层窗口内做 self-attention 就可以给第 l 层互相无重叠的窗口建立连接。
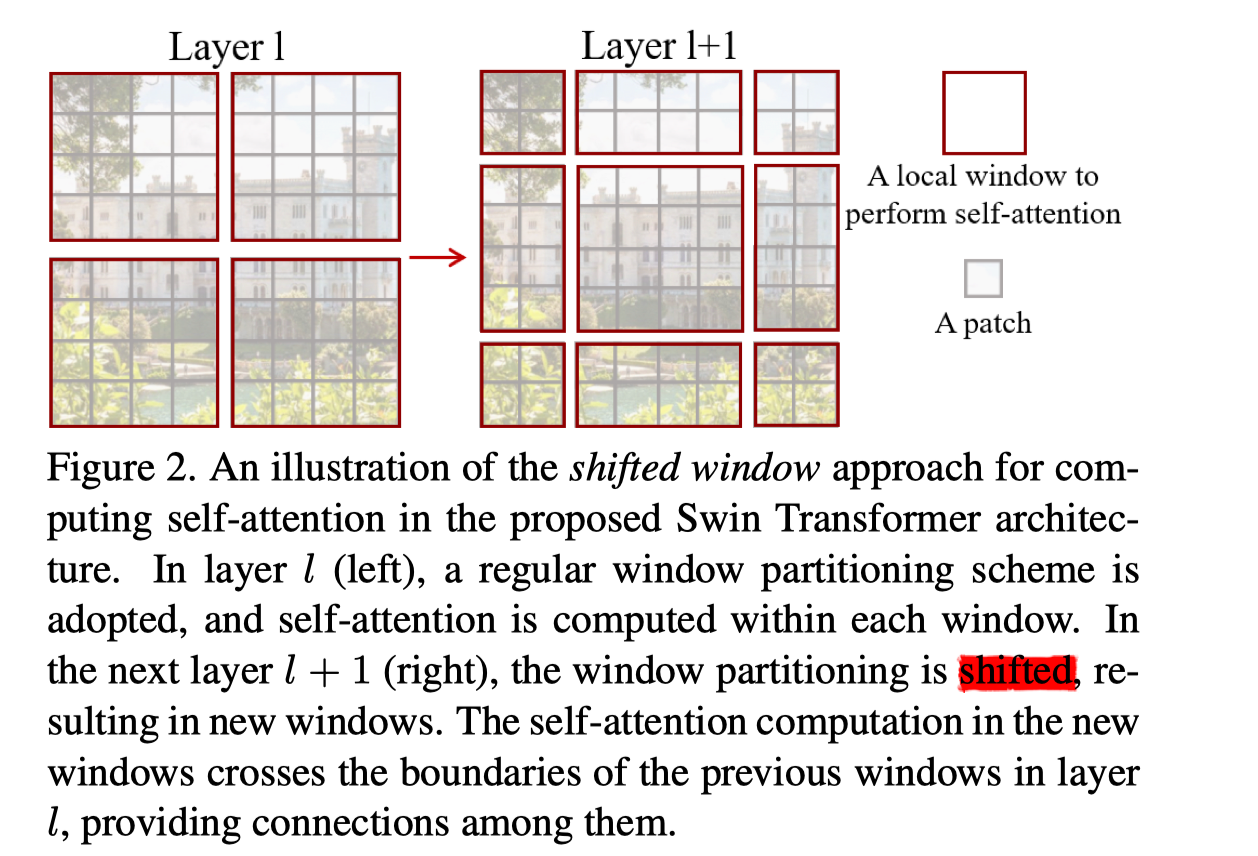
整体结构如图:
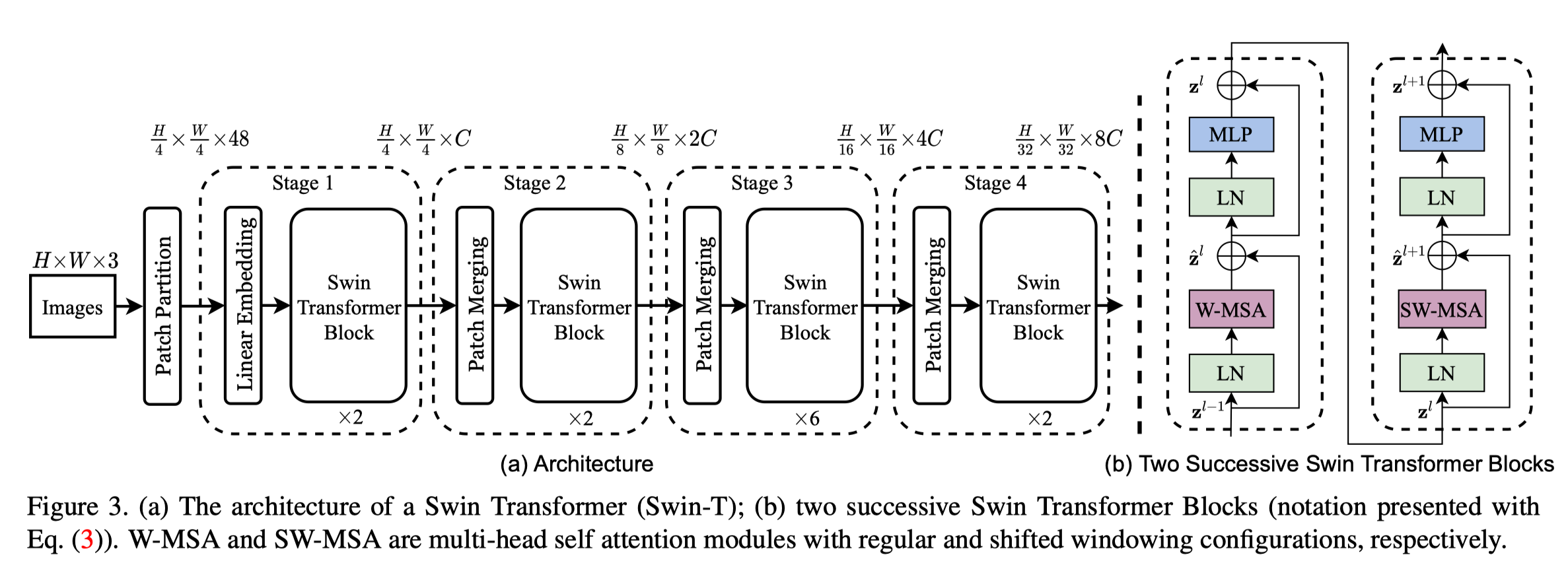
首先patch partition将输入按 4x4 切分为 patchs,得到 $ \frac{H}{4}\times{\frac{W}{4}}\times{48}$, 然后进入 Stage 1, 先是 linear Embedding 把channel 变成 C, 然后进入 Swin Transformer Block, 其结构如图3(b) 所示, 和ViT主要区别是用 W-MSA 和 SW-MSA 替换了普通的 MSA。
$$ \begin{array}{l}\hat{\mathbf{z}}^{l}=\mathrm{W}-\mathrm{MSA}\left(\mathrm{LN}\left(\mathbf{z}^{l-1}\right)\right)+\mathbf{z}^{l-1} \ \mathbf{z}^{l}=\operatorname{MLP}\left(\operatorname{LN}\left(\hat{\mathbf{z}}^{l}\right)\right)+\hat{\mathbf{z}}^{l} \ \hat{\mathbf{z}}^{l+1}=\mathrm{SW}-\operatorname{MSA}\left(\operatorname{LN}\left(\mathbf{z}^{l}\right)\right)+\mathbf{z}^{l} \ \mathbf{z}^{l+1}=\mathrm{MLP}\left(\mathrm{LN}\left(\hat{\mathbf{z}}^{l+1}\right)\right)+\hat{\mathbf{z}}^{l+1}\end{array} $$
然后进入 stage2 stage3 stage4, 每个 stage 都是在先对 patch 做合并,feature 长宽减半,然后接 swin transofer block。
cycle shift:
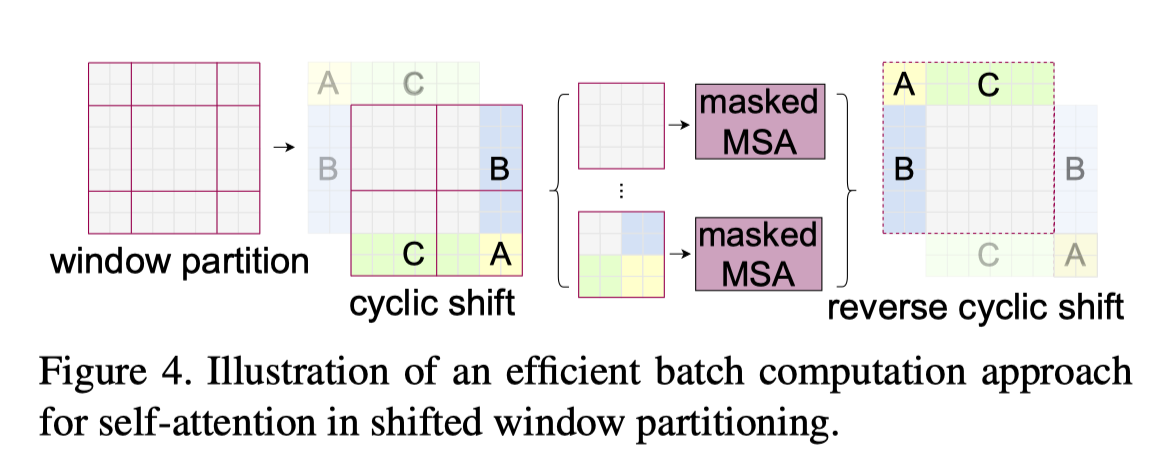
relative position bias: $$ \operatorname{Attention}(Q, K, V)=\operatorname{SoftMax}\left(Q K^{T} / \sqrt{d}+B\right) V $$