Structure-Coherent Deep Feature Learning for Robust Face Alignment 链接到标题
* Authors: [[Chunze Lin]], [[Beier Zhu]], [[Quan Wang]], [[Renjie Liao]], [[Chen Qian]], [[Jiwen Lu]], [[Jie Zhou]]
初读印象 链接到标题
soft wingloss 使用图网络建模关键点之间的联系,同时提出一种 relative location loss 强化关键点相互之间的关联信息,以及 soft wing loss 强化绝点坐标的学习。
难样本的标注难免不精确,而wingloss在小损失下的大梯度会导致模型强行拟合标注误差
TL;DR 链接到标题
使用图网络建模关键点之间的联系,同时提出一种 relative location loss 强化关键点相互之间的关联信息,以及 soft wing loss 强化绝点坐标的学习。这些方法的结合强化了模型在难样本(比如大角度和大遮挡)下的表现。
方法 链接到标题
使用图网络建模关键点关联 链接到标题
为什么要用图模型 链接到标题
 如上图所示, fc 的每个输出都和共同的 hidden features 作用,这使得每个关键点都互相强相关,这样在难样本下,如果一个关键点预测错了,所有其他关键点都会受到它的影响。
如上图所示, fc 的每个输出都和共同的 hidden features 作用,这使得每个关键点都互相强相关,这样在难样本下,如果一个关键点预测错了,所有其他关键点都会受到它的影响。
而人脸关键点之间有着明确的相对位置关系,即使部分点被遮挡了依托部分相邻的点也可以猜出大概,这个场景是典型的 GCN 适用的场景。
如何做 链接到标题
Node Embeding 首先用传统 DNN 提取图片 feature map $F \in \mathbb{R}^{C \times H \times W}$ , 但是 GCN 需要的输入数量是关键点数量的整数倍,所以后面加了两个 Conv-BN-ReLU 模块将卷积特征转换为隐层特征 $\boldsymbol{H}=\phi(\boldsymbol{F}) \in \mathbb{R}^{N n \times H \times W}$ , 其中 $N$ 为关键点数量,$n$ 为特征放大倍数。 接着把 $H$ reshape 得到 $H^0 \in \mathbb{R}^{N \times n H W}$ 作为 GCN 的输入 feature。
Sparse Graph Construction 构造稀疏图
统计邻居节点 计算数据集所有gt 关键点之间的皮尔森相关系数 $$\boldsymbol{C}=\frac{1}{2}\left(\operatorname{abs}\left(\boldsymbol{C}{x}\right)+\operatorname{abs}\left(\boldsymbol{C}{y}\right)\right)$$ 其中 $\boldsymbol{C}{x} \in \mathbb{R}^{N \times N}$ 和 $\boldsymbol{C}{y} \in \mathbb{R}^{N \times N}$ 分别是 x 坐标和 y 坐标的相关系数矩阵。 每行取最大的 k+1 个值构造稀疏图 $$ \boldsymbol{M}{i j}= \begin{cases}1, & \text { if } \boldsymbol{C}{i j} \in \operatorname{Top}{t=1, \ldots, N}^{k+1}\left(\boldsymbol{C}{i t}\right) \ 0, & \text { otherwise }\end{cases}$$
动态调整矩阵权重 上面的 $M$ 是个二值矩阵,意味着每个关键点贡献度一样, 但是实际上随着人脸角度、遮挡变化, 关键点的重要性也是在变化的。因此,我们需要将 $M$ 修改为随着输入特性改边的矩阵。具体做法是在前面的 $H^0$ 后面接一个 GAP 和两个 fc, fc 的输出长度为二值 $M$ 中非 0 元素的个数。最后用学到的 fc 参数替代对应位置的 1.
Graph Relational Layers
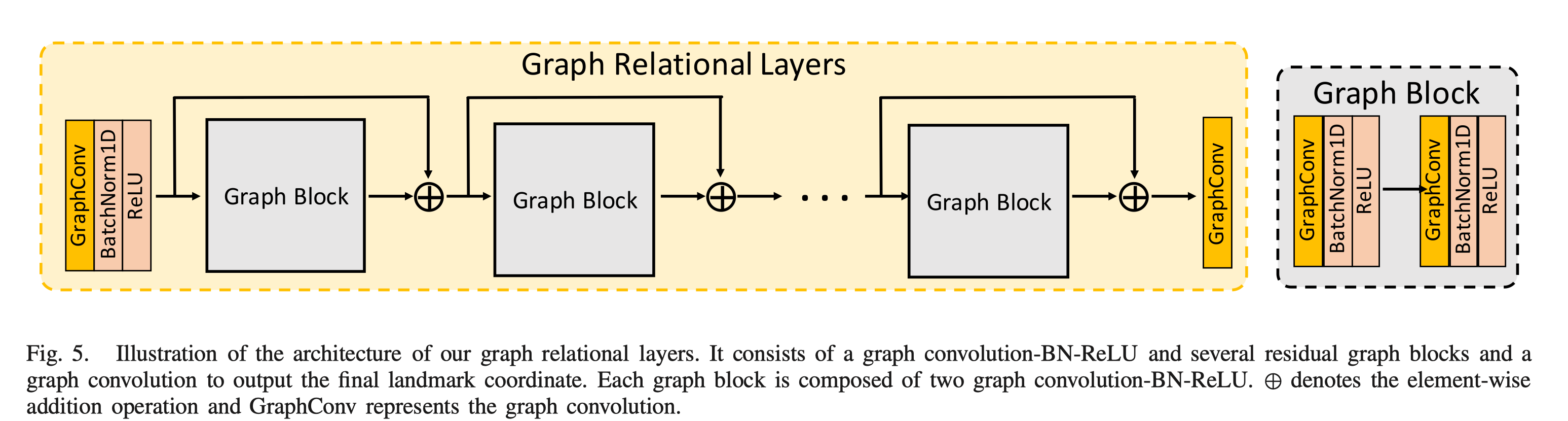 将 $H^0$ 和 稀疏矩阵输入上图所示的 Graph Relational Layers , 并使最后一个层的输出 $\boldsymbol{P} \in \mathbb{R}^{N \times 2}$ 就得到了预测的关键点坐标。
将 $H^0$ 和 稀疏矩阵输入上图所示的 Graph Relational Layers , 并使最后一个层的输出 $\boldsymbol{P} \in \mathbb{R}^{N \times 2}$ 就得到了预测的关键点坐标。
损失函数
Relative location Loss 传统方法只约束绝对位置损失,但是相对位置损失同样重要,因为相对位置蕴藏着人脸的结构信息。因此使用下面的拉普拉斯先验 $$\boldsymbol{\delta}{\boldsymbol{i}}=\sum{j \in \mathcal{N}{i}} \omega{i j}\left(\boldsymbol{p}{\boldsymbol{i}}-\boldsymbol{p}{\boldsymbol{j}}\right)=\boldsymbol{p}{\boldsymbol{i}}-\sum{j \in \mathcal{N}{i}} \omega{i j} \boldsymbol{p}{\boldsymbol{j}} $$ 其中 $\sum{j \in \mathcal{N}{i}} \omega{i j}=1$ , 表示关键点与邻居点之间的权重, 文中简单取邻居点个数的倒数 $\omega_{i j}=\frac{1}{\left|\mathcal{N}{i}\right|}$ 作为权重,通过最小化预测关键点的 $\hat{\boldsymbol{\delta}}{i}$ 和 gt 的 $\boldsymbol{\delta}{i}$ , 就达到了约束相对位置的作用。 实际计算的时候构造 N 个关键点的拉普拉斯矩阵 $$\boldsymbol{L}{i, j}= \begin{cases}-\omega_{i j} & \text { if } j \in \mathcal{N} i \ 1 & \text { if } i=j \ 0 & \text { otherwise }\end{cases}$$ 所有关键点用 $\boldsymbol{P} \in \mathbb{R}^{N \times 2}$ 表示, 那么 $\Delta=\left[\boldsymbol{\delta}{\mathbf{1}}, \boldsymbol{\delta}{\mathbf{2}}, \cdots, \boldsymbol{\delta}_{\boldsymbol{N}}\right]^{T}$ 可以用矩阵乘方便地计算得到 $$\Delta=\boldsymbol{L} \boldsymbol{P}$$
Soft Wing Loss $$\operatorname{SoftWing}(x)= \begin{cases}|x| & \text { if }|x|<\omega_{1} \ \omega_{2} \ln \left(1+\frac{|x|}{\epsilon}\right)+B & \text { otherwise }\end{cases}$$ 该 loss 是用来约束绝对坐标的, 我们知道 L2 loss 专注于 large errors 而忽视了 small errors,因此提出了上面的 soft wing loss 形式。当误差较小时采用 L1 loss 的形式, 当误差较大时采用对数形式。 对比一下 wing loss 的形式: $$\operatorname{Wing}(x)= \begin{cases}\omega \ln \left(1+\frac{|x|}{\epsilon}\right) & \text { if }|x|<\omega \ |x|-C & \text { otherwise }\end{cases}$$ 整体看起来还挺像的,但实际差距很大,wing loss 在小误差下是对数形式,大误差下是 L1 形式(小误差时大梯度, 大误差时梯度恒定为1),而 soft wing loss 则是反过来的(小误差下梯度恒定为1,大误差下对数梯度 )。之所以这个形式, 是因为在作者的实验中 wingloss 不是一直好于 L1,尤其是在难样本比较多的 WFLW 数据集上, 可能原因是__难样本的标注难免不精确,而wingloss在小损失下的大梯度会导致模型强行拟合标注误差__。而 softwing loss 的形式可以方便地控制在中误差 $\omega_{1}<|x|<\omega_{2}$ 和大误差 $|x|>\omega_{2}$ 下的梯度,并且由于整个函数的梯度都维持在 $\left[\frac{\omega_{2}}{C}, 1\right]$ 之间, 不会给离群点特别大的梯度,因此对数据噪声是不敏感的。
实验结果 链接到标题
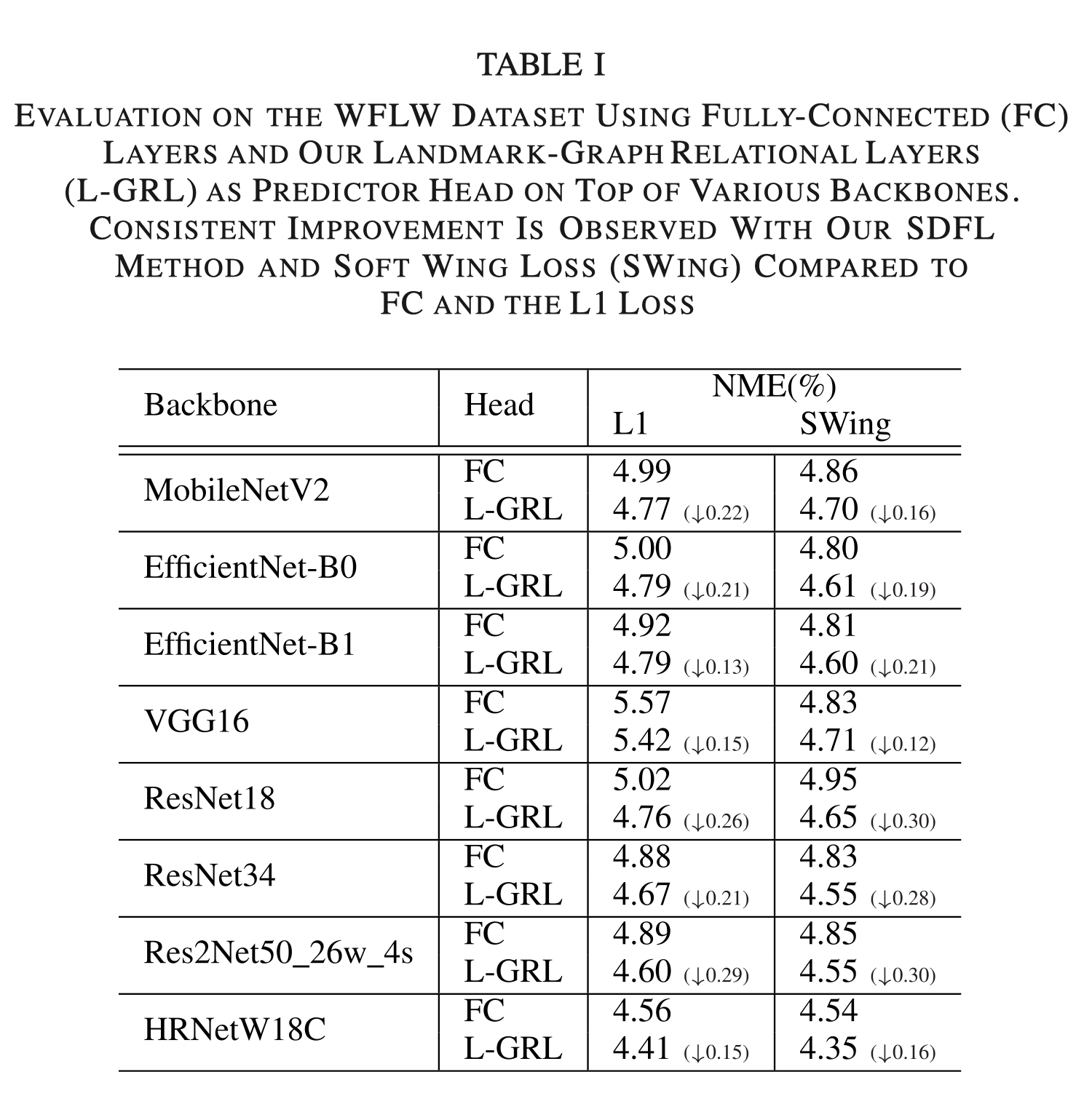


References 链接到标题
- This reference does not have DOI 😵
- This reference does not have DOI 😵
- 10.1109/TPAMI.2020.2983935
- 10.1109/CVPR42600.2020.00590
- 10.1109/CVPR.2019.00358
- 10.1007/978-3-319-10599-4_7
- This reference does not have DOI 😵
- 10.1109/MSP.2017.2693418
- 10.1109/TNN.2008.2005605
- 10.1109/ICCV.2019.00087
- 10.1109/CVPR.2016.373
- 10.1109/CVPR.2017.606
- 10.1007/978-3-319-46448-0_4
- 10.1109/CVPR.2017.392
- 10.1109/CVPR.2010.5539996
- 10.1109/CVPR.2019.00360
- 10.1109/CVPR.2014.306
- 10.1109/CVPR.2018.00047
- [[@kumarLUVLiFaceAlignment2020]]
- 10.1109/TPAMI.2009.167
- 10.1109/CVPR.2018.00052
- 10.1109/CVPR.2018.00045
- 10.1109/TPAMI.2019.2907634
- [[@fengWingLossRobust2018]]
- [[@wuLookBoundaryBoundaryAware2018b]]
- 10.1109/CVPR.2016.90
- This reference does not have DOI 😵
- 10.1109/TPAMI.2019.2938758
- 10.1109/AFGR.1998.670965
- 10.1109/34.927467
- 10.1007/s11263-010-0380-4
- 10.5244/C.20.95
- 10.1109/CVPR.2019.00354
- 10.1145/1057432.1057456
- 10.1109/TIP.2015.2446944
- This reference does not have DOI 😵
- 10.5244/C.29.22
- 10.1109/ICCV.2019.00707
- 10.1109/ICCV.2019.01025
- 10.1109/ACCESS.2019.2930304
- 10.1109/CVPR42600.2020.00615
- 10.1109/TPAMI.2013.23
- 10.1145/2929464.2929475
- 10.1109/CVPRW.2017.253
- This reference does not have DOI 😵
- 10.1109/CVPR.2019.00584
- 10.1109/CVPR.2016.453
- This reference does not have DOI 😵
- 10.1007/978-3-319-46484-8_29
- 10.1109/ICCV.2013.191
- 10.1016/j.imavis.2016.01.002
- 10.1109/CVPR.2018.00474
- This reference does not have DOI 😵
- 10.1109/CVPRW.2017.261
- [[@dapognyDeCaFADeepConvolutional2019]]
- 10.1109/TIP.2017.2657118
- 10.1109/TIP.2016.2518867
- This reference does not have DOI 😵
- 10.1109/TIP.2016.2633939
- 10.1109/CVPR.2018.00275
- 10.1109/CVPR.2018.00735
- 10.1109/CVPR.2019.00857
- 10.1007/978-3-030-01246-5_41
- 10.1109/CVPR.2019.00952
- 10.1109/CVPR.2019.00307
- This reference does not have DOI 😵
- This reference does not have DOI 😵
- 10.1109/TIP.2020.3028207
- 10.1109/ICCV.2017.556
Currently 4 references inside library! @2022-12-28