Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection 链接到标题
* Authors: [[Xiang Li]], [[Wenhai Wang]], [[Lijun Wu]], [[Shuo Chen]], [[Xiaolin Hu]], [[Jun Li]], [[Jinhui Tang]], [[Jian Yang]]
初读印象 链接到标题
通过结合框质量分和框分类分的同时使用概率分布替代狄拉克分布形式的边界框解决了当前检测框架中存在的训练测试不统一以及框表示不灵活的两个问题。
URL 链接到标题
https://arxiv.org/pdf/2006.04388.pdf
TL;DR 链接到标题
通过结合框质量分和框分类分的同时使用概率分布替代狄拉克分布形式的边界框解决了当前检测框架中存在的训练测试不统一以及框表示不灵活的两个问题。
Dataset/Algorithm/Model/Experiment Detail 链接到标题
首先作者提出了当前 FCOS ATSS 等一阶段检测方法存在的两个显著问题:
框质量分和框分类分数在训练和测试中的使用方式是不统一的
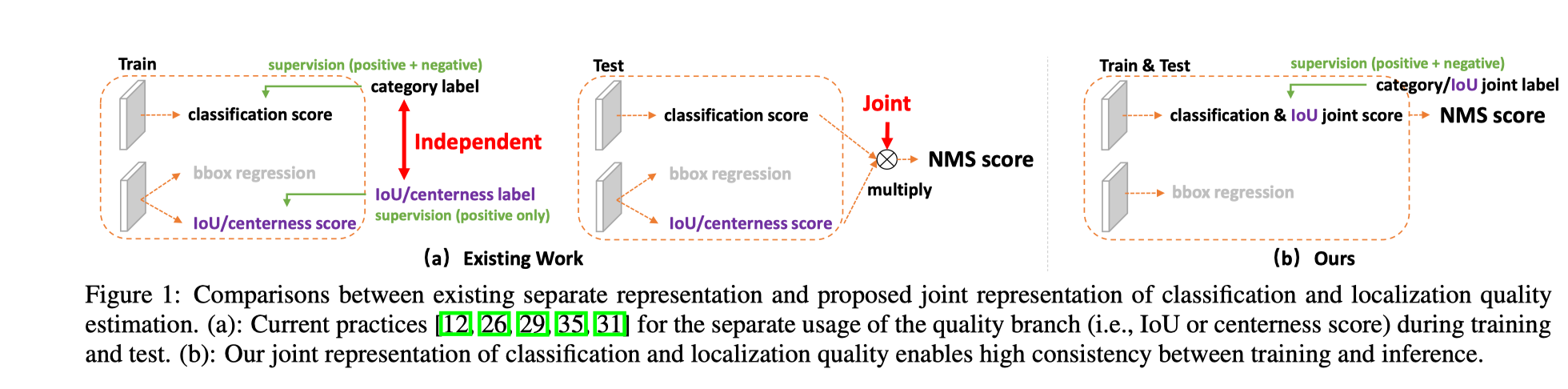
训练的时候分类分数和框质量分学习、使用是相互独立的, 但是测试的时候是将两者相乘作为 NMS 框排序依据的
框质量分只能对正样本计算,而框分类分数对正负样本的都可以计算
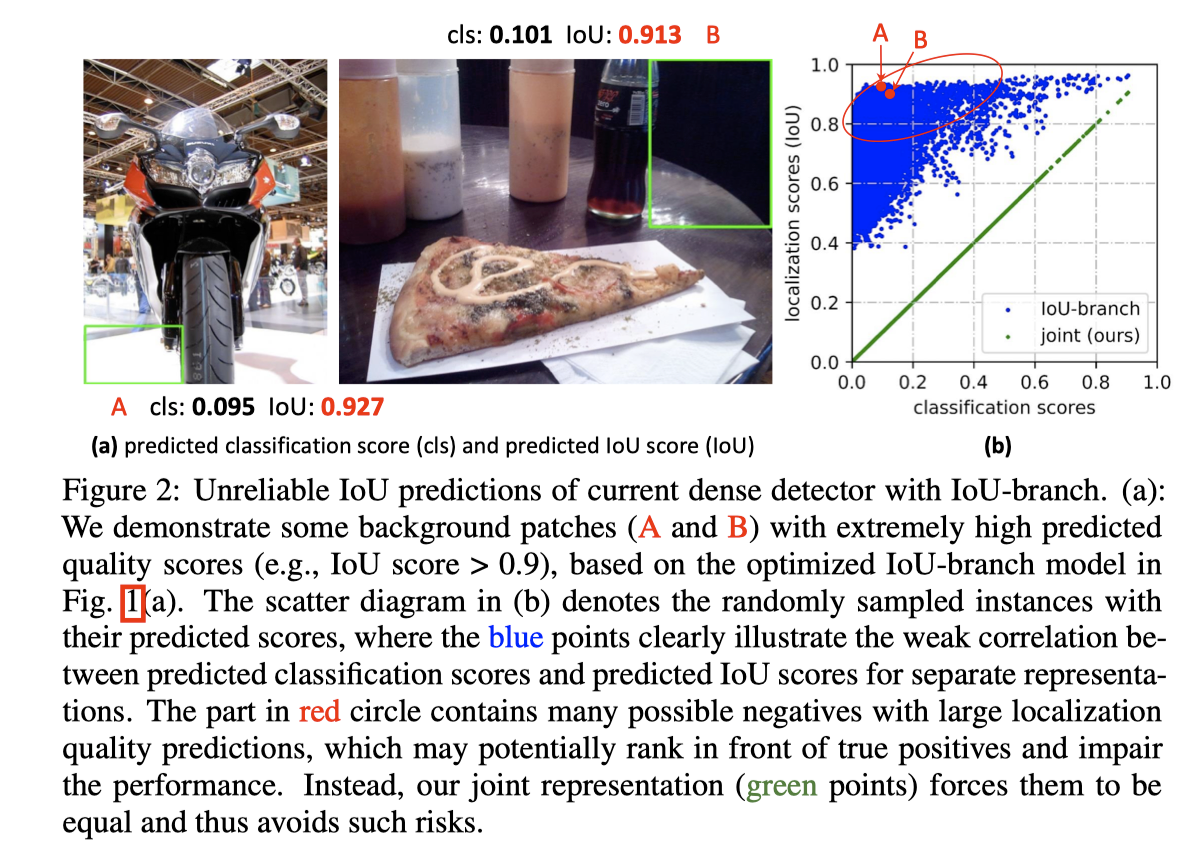
这导致的如下图所示的问题: 如果一个背景框虽然分类分数已经给的很低了,但是它和 gt 之间的 IoU 仍然可能很大,当两者相乘之后的分数有可能会大于普通正样本的分数,导致这个框在 NMS 的时候排在前面造成 FP。
当前回归框的表示不够灵活
当前框表示可以看成是一个狄拉克分布,我们认为在框内的就是属于目标,框外就不属于目标,即只存在 0、1两种状态,中间没有过度。但是实际情况并不是那么简单,比如下面的图,因为阴影、遮挡等各种情况,目标的边界并不足够清晰,我们无法标出绝对准确的框,这个时候狄拉克分布去强行拟合反而是不好的。

针对上面的两个问题,作者针对性提出了解决办法
合并框质量分表示和框分类分的表示 (classification-IoU joint representation)
修改 one-hot 编码, 原来目标类对应序号位置的值为 1, 现在将它设为框的质量分。特别的, 对于负样本这个值设为 0。
使用不依赖先验的概率分布替代狄拉克分布表示框坐标 ( General distribution )
它们与已有方法对比如下图
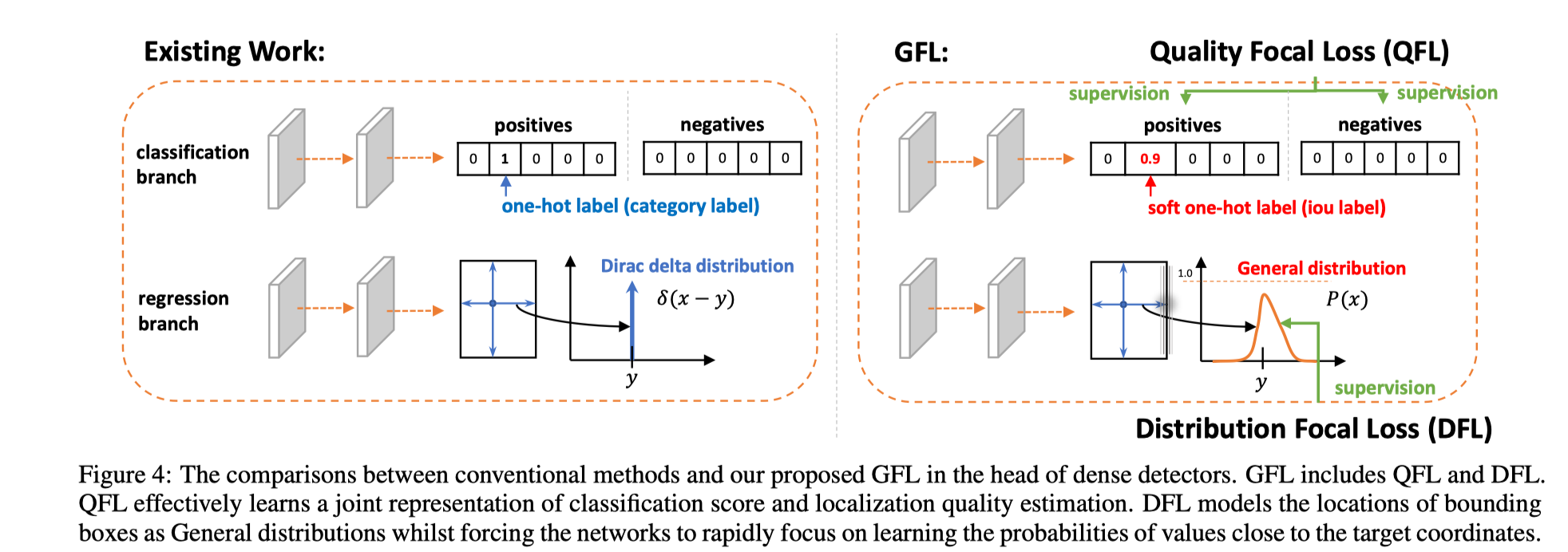
进一步地,作者基于这两种表示形式的改进,提出了相对应的两种新的 Focal Loss 表示: Quality Focal Loss (QFL) 和 Distribution Focal Loss (DFL)。然后将两者结合形成了一个统一的 loss 形式: Generalized Focal Loss (GFL)。下面对它们分别介绍:
Quality Focal Loss 链接到标题
我们知道 Focal Loss 的形式如下:
$\mathbf{F L}(p)=-\left(1-p_{t}\right)^{\gamma} \log \left(p_{t}\right), p_{t}=\left{\begin{aligned} p, & \text { when } y=1 \ 1-p, & \text { when } y=0 \end{aligned}\right.$
这个 loss 形式需要标签是 0-1 形式的, 由于作者将框分类分和质量分的表示进行了联合,这个原始的 Focal Loss 形式已经不能使用, 为此,首先将它的形式进行展开得到 $-((1-y) \log (1-\sigma)+y \log (\sigma))$ , 然后使用过 softmax 的输出和上面的连续标签的距离 $|y-\sigma|^\beta$ 替代 $(1-p_t)^\gamma$ 这一项。所以,最终形式是:
$\mathbf{Q F L}(\sigma)=-|y-\sigma|^{\beta}((1-y) \log (1-\sigma)+y \log (\sigma))$
不同 $\beta$ 下它的曲线如下
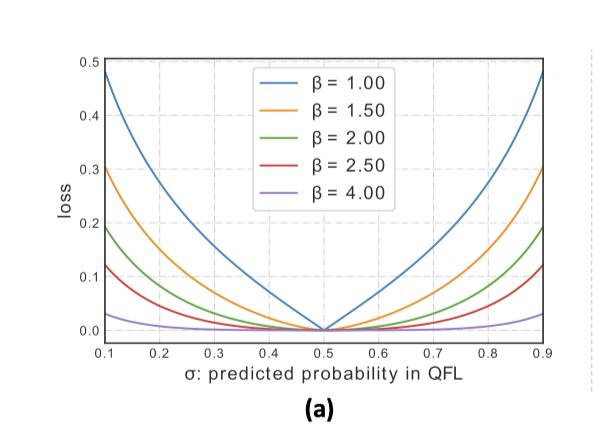
作者的实验里 $\beta=2$ 效果最好。
Distribution Focal Loss 链接到标题
传统方法将框坐标 y 坐标回归建模成狄拉克分布,从中恢复为 y 的方式用下式表示。
$y=\int_{-\infty}^{+\infty} \delta(x-y) x \mathrm{~d} x$
本文作者比对这个分布做任何假设,定义任意一个在 y 附近 $[y_0, y_n]$ 分布函数 $P(x)$
$\hat{y}=\int_{-\infty}^{+\infty} P(x) x \mathrm{~d} x=\int_{y_{0}}^{y_{n}} P(x) x \mathrm{~d} x$
为了符合 cnn 的表示, 将这个区间离散化为 $\left{y_{0}, y_{1}, \ldots, y_{i}, y_{i+1}, \ldots, y_{n-1}, y_{n}\right}$ , 他们的间隔用 $\Delta$ 表示。 如果给定各个点的概率 $\sum_{i=0}^{n} P\left(y_{i}\right)=1$ 就可以算出回归坐标 $\hat{y}=\sum_{i=0}^{n} P\left(y_{i}\right) y_{i}$ 。其中 $P(x)$ 可以使用包含 n+1 个 units 的 softmax 来得到。满足这个条件的分布有很多,直接学的话效率不高, 直觉上,这个分布应该, 这个分布应该张得像第 3 个分布, 即约靠近 gt 的概率应该更高,
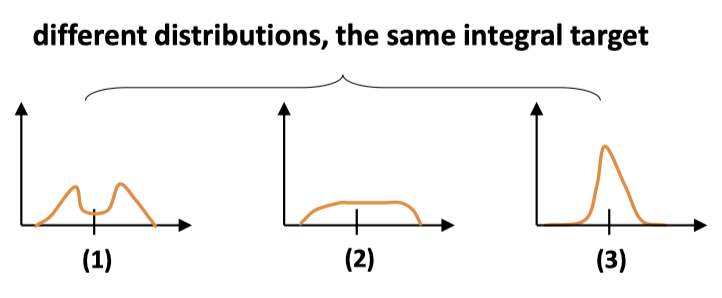
为了得到这样一个分布,作者提出了下面的 DFL 形式:
$\mathbf{D F L}\left(\mathcal{S}{i}, \mathcal{S}{i+1}\right)=-\left(\left(y_{i+1}-y\right) \log \left(\mathcal{S}{i}\right)+\left(y-y{i}\right) \log \left(\mathcal{S}_{i+1}\right)\right)$
其中 $y_i$ 和 $y_{i+1}$ 为靠 y 最近的两个点。当 $\mathcal{S}{i}=\frac{y{i+1}-y}{y_{i+1}-y_{i}}, \mathcal{S}{i+1}=\frac{y-y{i}}{y_{i+1}-y_{i}}$ 时可以获得全局最小值。此时回归坐标 $\hat{y}$ 无限接近 y。
Generalized Focal Loss (GFL) 链接到标题
结合 QFL 和 DFL 得到下面的形式:
$\mathbf{G F L}\left(p_{y_{l}}, p_{y_{r}}\right)=-\left|y-\left(y_{l} p_{y_{l}}+y_{r} p_{y_{r}}\right)\right|^{\beta}\left(\left(y_{r}-y\right) \log \left(p_{y_{l}}\right)+\left(y-y_{l}\right) \log \left(p_{y_{r}}\right)\right)$
作者实际训练时采用的是下面的形式
$\mathcal{L}=\frac{1}{N_{p o s}} \sum_{z} \mathcal{L}{\mathcal{Q}}+\frac{1}{N{p o s}} \sum_{z} \mathbf{1}{\left{c{z}^{*}>0\right}}\left(\lambda_{0} \mathcal{L}{\mathcal{B}}+\lambda{1} \mathcal{L}_{\mathcal{D}}\right) $
其中 $L_B$ 为 GIoU loss。
比较分开结合“分类分分数和框质量分数”的效果
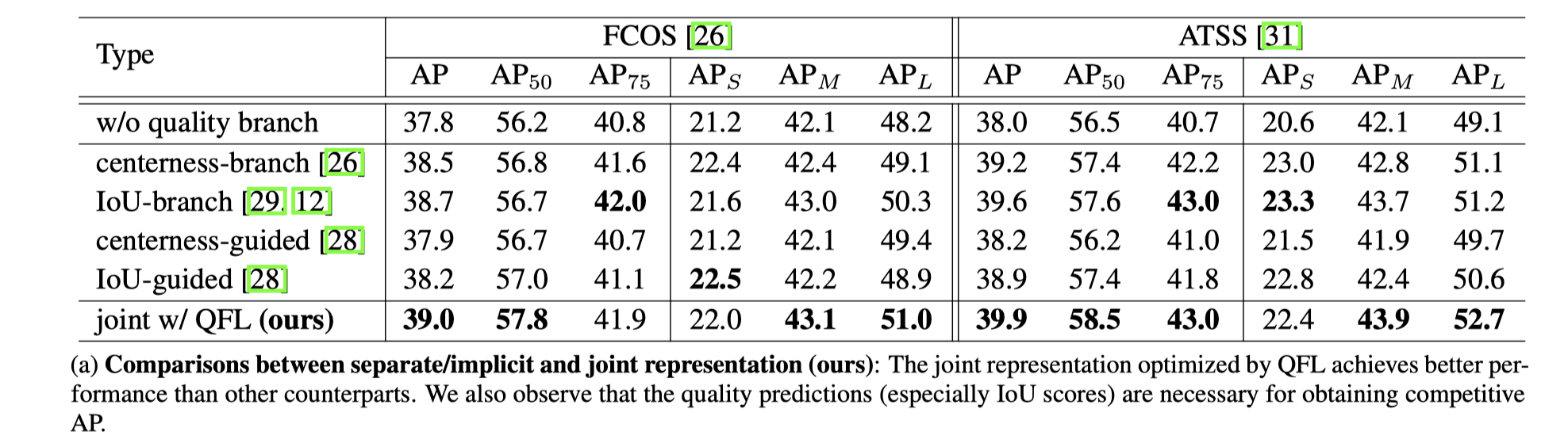
1 两者结合能获得更高的精度 2 框质量分不可或缺
各种 one-stage 框架上都能获得收益

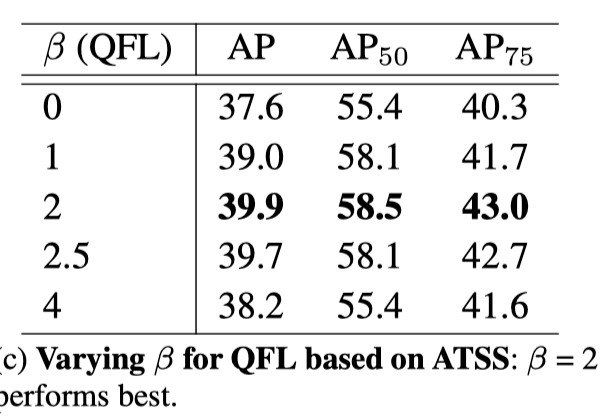
$\beta$ 参数的影响
作者的实验取 2 时效果最好
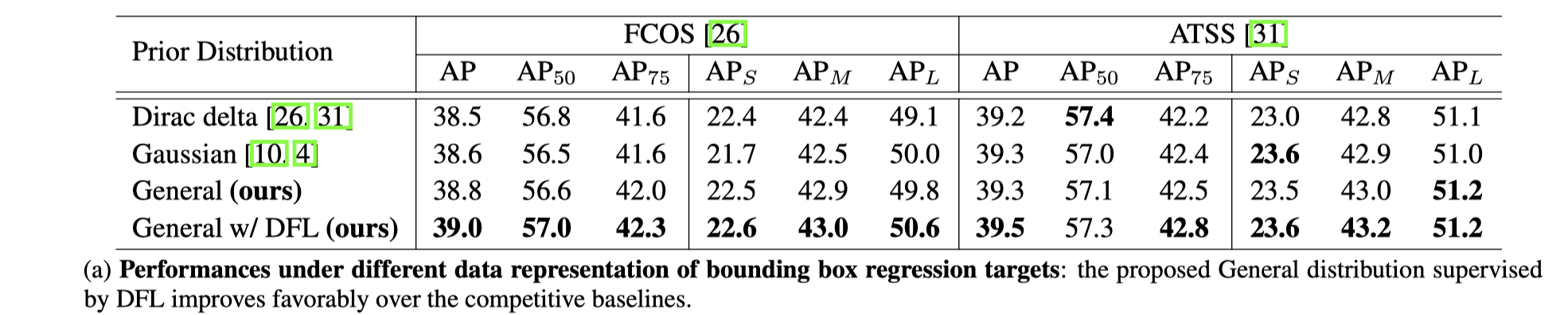
不同边框回归模型的效果
DFL 的效果要优于 dirac 和 gaussian 形式
固定采样步长下不同采样点数 n 对结果的影响
n 的选择对最终结果的影响不是很明显
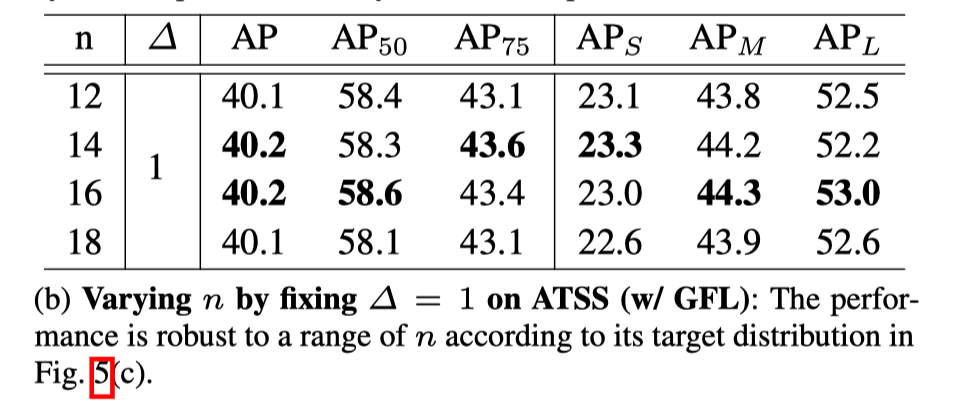
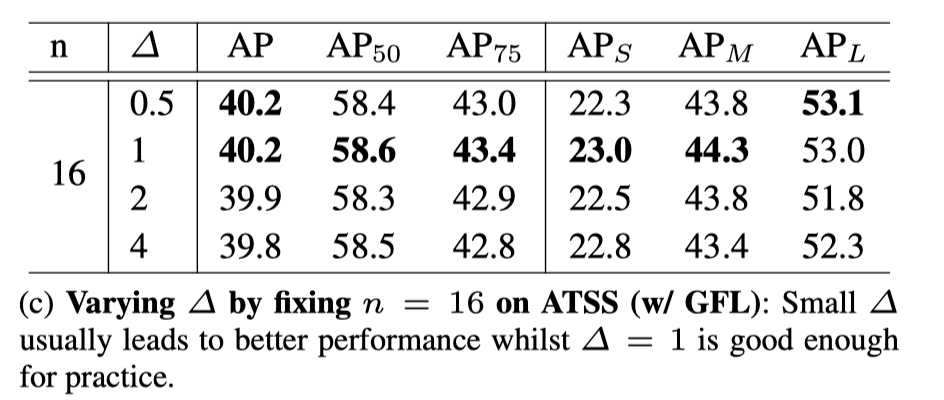
固定采样点个数下不同步长对结果的影响
整体上看,采样步长越小结果越好,作者最后取的 1。
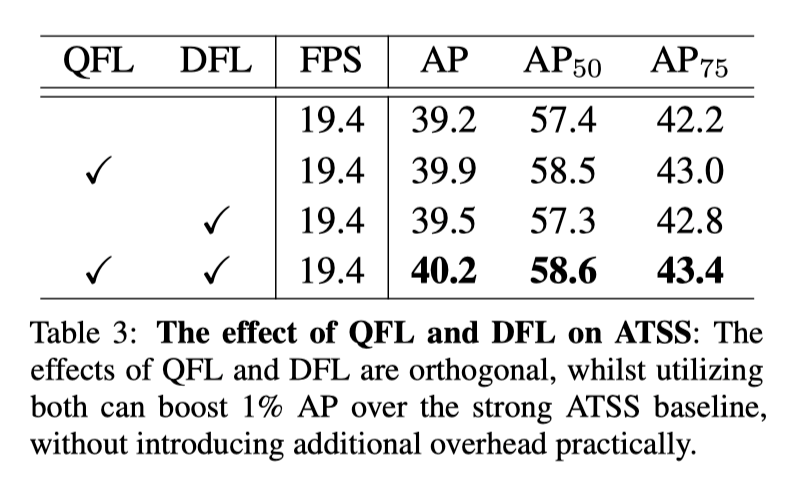
QFL 和 DFL 作用是相互正交的
他们的涨点效果可以叠加
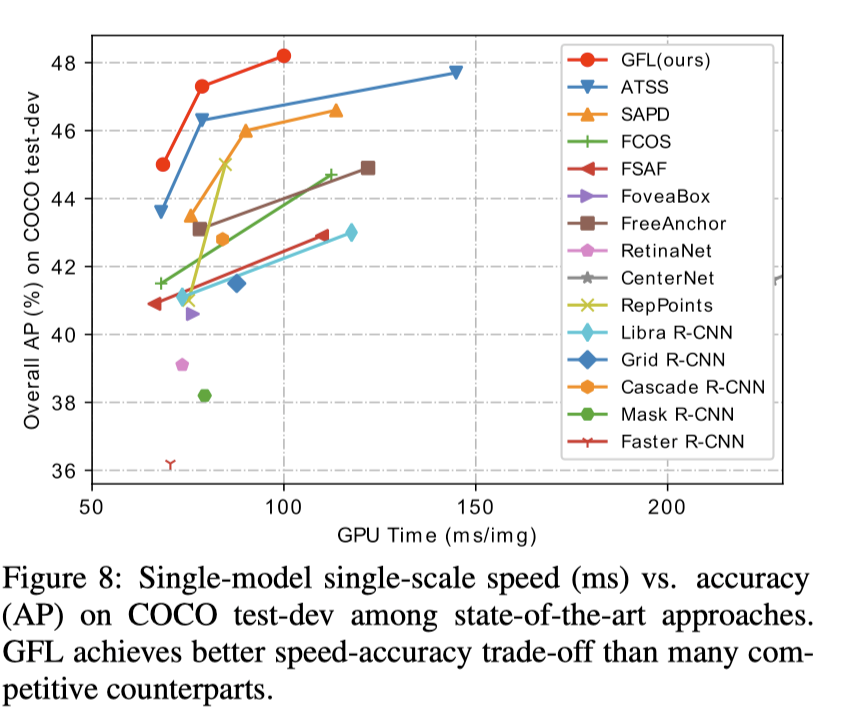
GFL 在 coco 数据集上将检测精度推向了新的高度
Thoughts 链接到标题
- 将边框回归变成回归问题来做很有意思
- 分类和质量分联合训练能够减小训练和测试之间的 gap, 使整个检测框架更加合理。