CLIFF: Carrying Location Information in Full Frames into Human Pose and Shape Estimation 链接到标题

* Authors: [[Zhihao Li]], [[Jianzhuang Liu]], [[Zhensong Zhang]], [[Songcen Xu]], [[Youliang Yan]]

初读印象 链接到标题

comment:: 引入 bounding box 的全局信息来解决 3d 人体姿态估计任务中全局旋转预测不准确的问题。

image.png

文章骨架 链接到标题

创新点是什么 链接到标题

novelty::

  1. 引入全局信息
  2. 在全图而不是 bounding box 上计算 loss
  3. 提出一种基于 CLIFF 的标注器

有什么意义 链接到标题

significance:: 解决人体 3d 姿态估计任务下人体全局朝向预测不准确的问题

有什么潜力 链接到标题

potential:: 1. 更精确的人体估计 2. 更少的标注成本

文章笔记 链接到标题

存在的问题 链接到标题

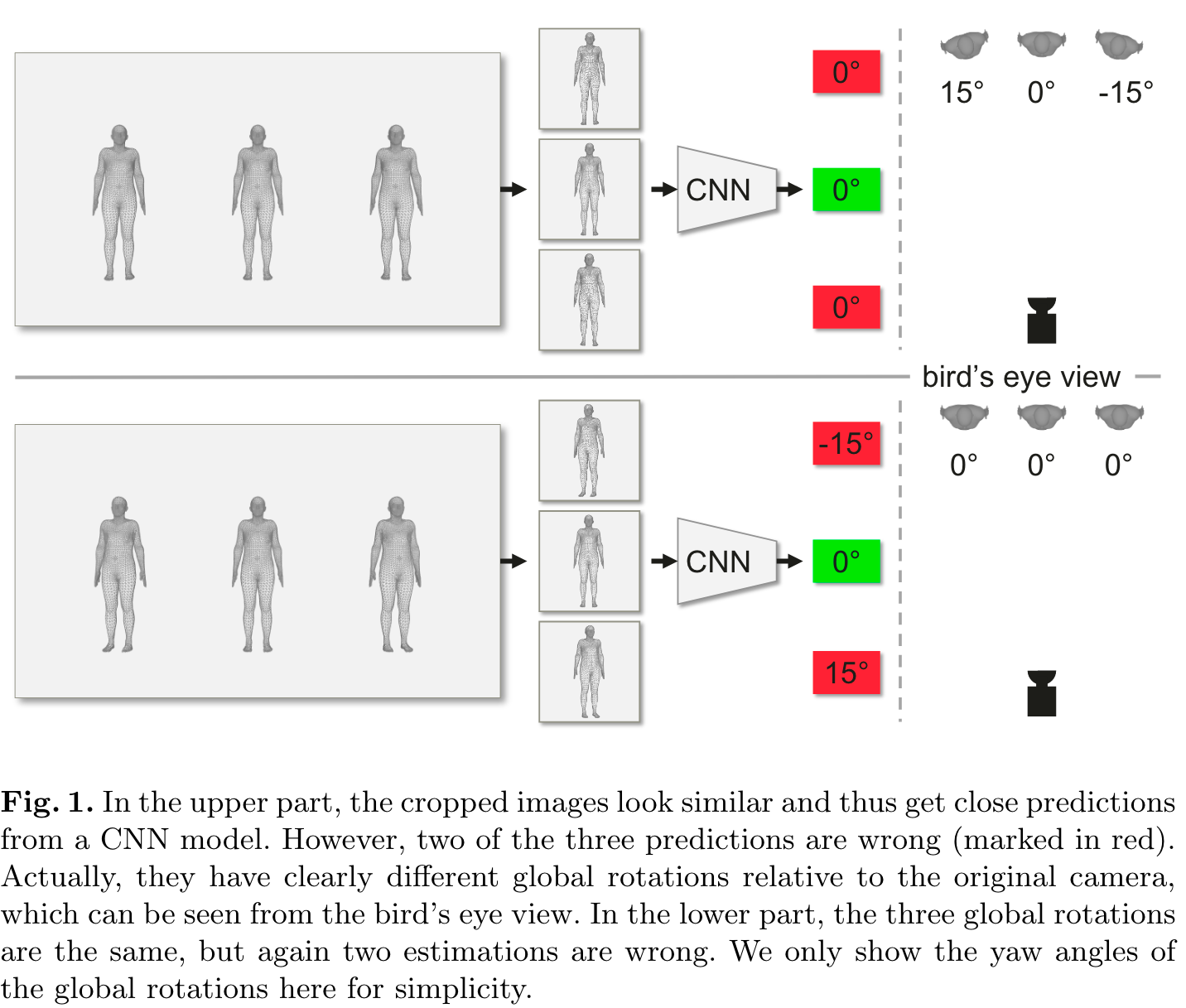
image.png

传统的 top-down 3d 人体姿态估计方法输入是抠完的人体框，这会丢失人体的全局朝向信息。 如图1所示， 上面这行的三个人等间距面朝相机的站立，从右侧的鸟瞰图上看三个人的实际的朝向并不相同，但是由于他们都是面向光心的，抠完的人体框成像上看起来朝向都是正前方的。下面这行三个人等距平行站立，实际朝向相同， 但是在抠完框的成像上三个人的朝向不同了。 显然如果基于丢失全局朝向抠框图预测姿态，映射回原图后就会和实际朝向存在偏差， 即使是现在 sota 的 top-dowm 模型也解决不了的问题。

解决问题的办法 链接到标题

作者解决的办法也很直接， 简单来说

  1. 给模型的输入加入 bounding box 在全图的坐标信息；
  2. 在计算回归 loss 的时候在全局计算而不是抠图内计算

一些基本知识

  1. SMPL 模型 一个参数化的人体模型， 输入是 $\Theta=\left{\boldsymbol{\theta},\boldsymbol{\beta}\right}$ 输出是 6890 个定点的 3d mesh。 其中 $\boldsymbol{\theta}\in\mathbb{R}^{2\tilde{4}\times3}$ 和 $\boldsymbol{\beta}\in\mathbb{R}^{10}$ 分别是 pose 和 shape 参数， $\theta$ 包括人体根节点（骨盆）相对坐标系的朝向以及 23 个关节相对父关节的局部旋转。其他感兴趣的 k 个节点可以通过预训练的稀疏矩阵和 mesh 定点的乘积获得：$J_{3D}=MV$ 。

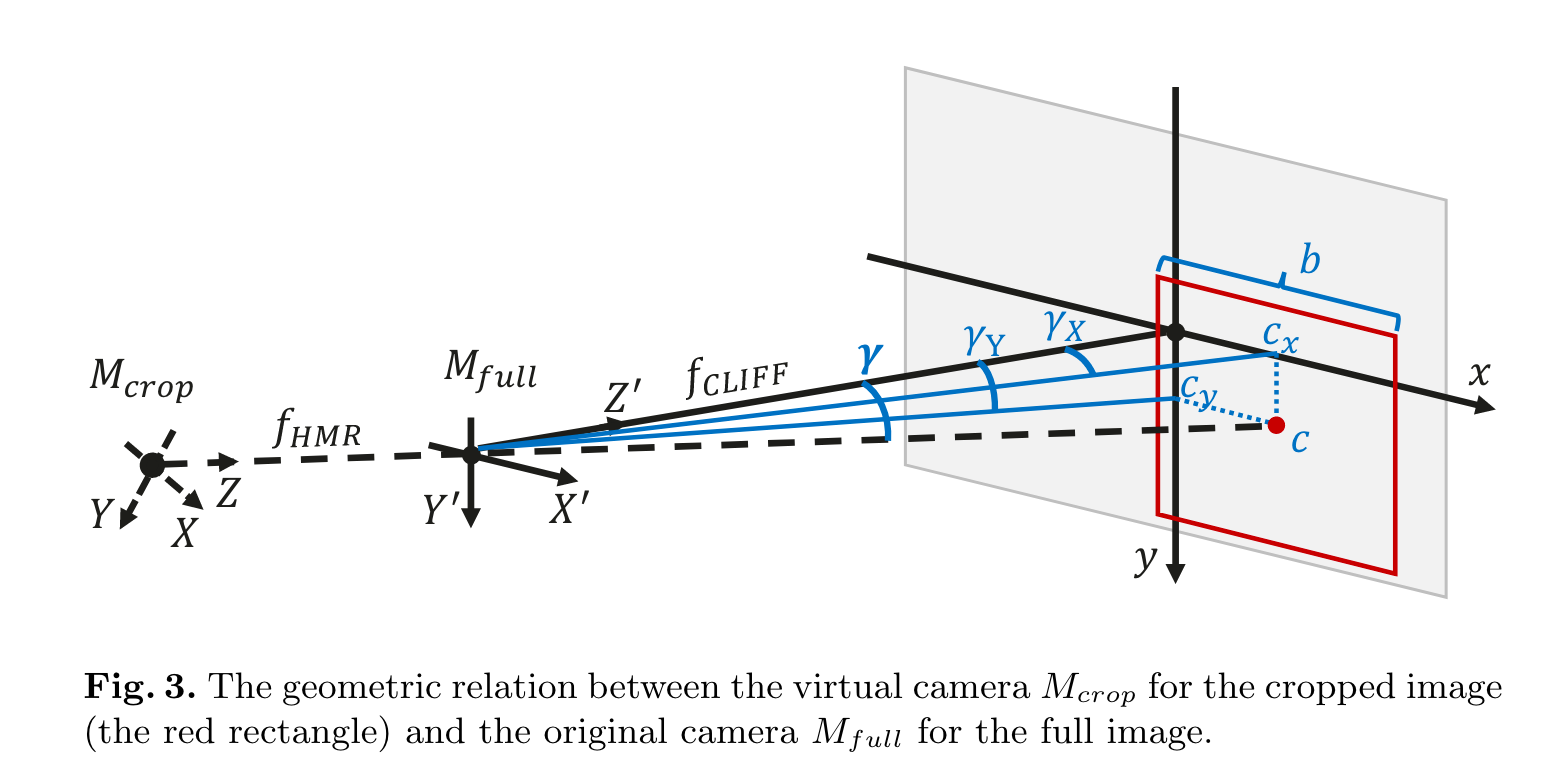
  2. HMR HMR 是一个结构简单且广泛使用的 top-down 人体 3d 模型，架构图如图 2(a) 所示， 首先抠出人体框并 resize 到 224x224 输入卷积编码器中， 然后输入 MLP 预测 SMPL 参数以及投影参数 $P_{weak}={s,t_x,t_y}$ , 如图3 定义一个以扣框中心为光心的虚拟相机，其中 $s$ 是在该坐标系统下 scale 系数， $t_x$ $t_y$ 是扣框中心全局中心的坐标偏移。如果预定义一个很大的焦距 $f_{HMR}=5000$ ， $P_{weak}$ 可以转化为投影参数 $P_{persp} = {f_{MHR}, t^{crop}}$ 其中 $\mathbf{t}^{crop}=[t_{X}^{crop},t_{Y}^{crop},t_{Z}^{crop}]$ 表示 $M_{crop}$ 相对全局在 x y z 坐标轴上的偏移。公式表示的话 $$t_{X}^{crop}=t_{x},t_{Y}^{crop}=t_{y},t_{Z}^{crop}=\dfrac{2\cdot f_{HMR}}{r\cdot s}$$ 其中 2 表示人体身高约数 2m， r=224 表示抠框的大小 224 像素，深度的公式可以通过简单的三角函数推导得到。损失函数 $$L^{HMR}=\lambda_{SMPL}L_{SMPL}+\lambda_{3D}L_{3D}+\lambda_{2D}L_{2D}^{crop}$$ $$J_{2D}^{crop}=\Pi J_{3D}^{crop}=\Pi(J_{3D}+\mathbf{1}\mathbf{t}^{crop})$$ $\Pi$ 为透视映射

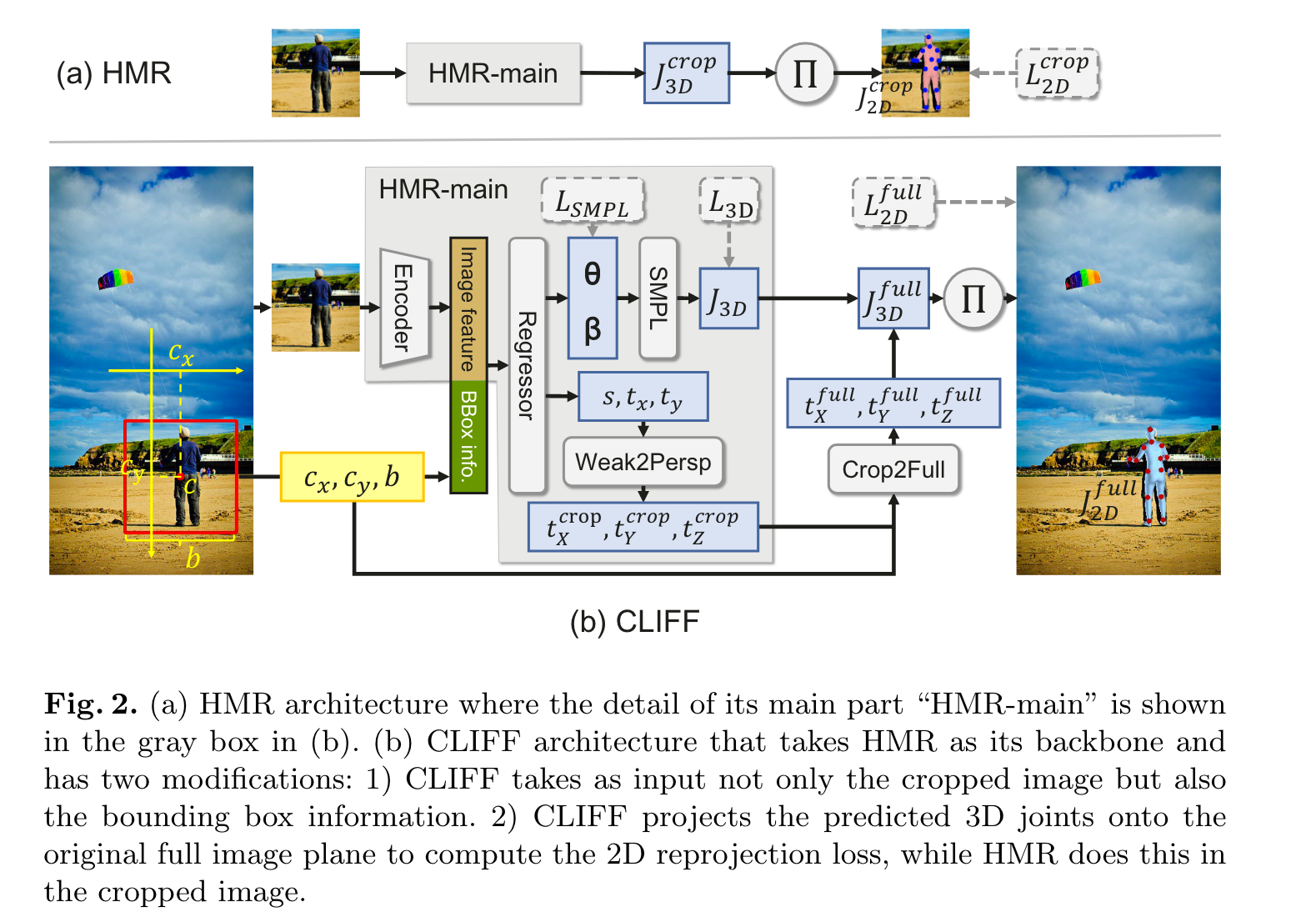
image.png

image.png

CLIFF

CLIFF 的结构如图2 (b) 所示，主要是增加了全局框位置和大小信息作为 MLP 的额外输入以及在计算 loss 时直接再全局 gt 上计算

$$I_{b b o x}=[\dfrac{c_{x}}{f_{CLIFF}},\dfrac{c_{y}}{f_{CLIFFF}},\dfrac{b}{f_{CLIFF}}]$$$c_x, c_y$ 是框中心相对全图中心的位置，$b$ 是框原始大小， $f_{CLIFF}$ 是原始相机的焦距，如果不知道焦距则用原始图片的对角线长度表示， $f_{CLIP}=\sqrt{w^2+h^2}$ 。 前两项实际上表示的是抠图框虚拟相机坐标系统相对全局相机系统坐标的正切：

$$\begin{aligned}\tan\gamma_X&=\frac{c_x}{f_{CLIFF}},\ \tan\gamma_Y&=\frac{c_y}{f_{CLIFF}},\end{aligned}$$ 同时计算 loss 时是在全局计算的，转换方式为：

$$\begin{aligned}t_{X}^{full}&=t_{X}^{crop}+\frac{2\cdot c_{x}}{b\cdot s},\ t_{Y}^{full}&=t_{Y}^{crop}+\frac{2\cdot c_{y}}{b\cdot s},\ t_{Z}^{full}&=t_{Z}^{crop}\cdot\frac{fCLIFF}{f_{YMR}}\cdot\frac{r}{b}\end{aligned}$$ loss 计算： $$L_{2D}^{full}=\left\Vert J_{2D}^{full}-\hat J_{2D}^{full}\right\Vert$$ $$L^{CLIFF}=\lambda_{SMPL}L_{SMPL}+\lambda_{3D}L_{3D}+\lambda_{2D}L_{2D}^{full}$$

基于 CLIFF 的标注器 链接到标题

  1. 在有 SMPL gt 的数据集上预训练 CLIFF, 作为第三步的隐式先验；
  2. 在目标数据集上跑预训练 CLIFF, 得到的输出作为明确先验， 标注员只要在上面微调就行；
  3. 使用2d 关键点作为弱监督信号，在目标数据集上 finetune CLIFF，获得更新的标注器。
  4. 在目标数据集上跑 finetune 的 CLIFF 作为 gt。

实验结果 链接到标题

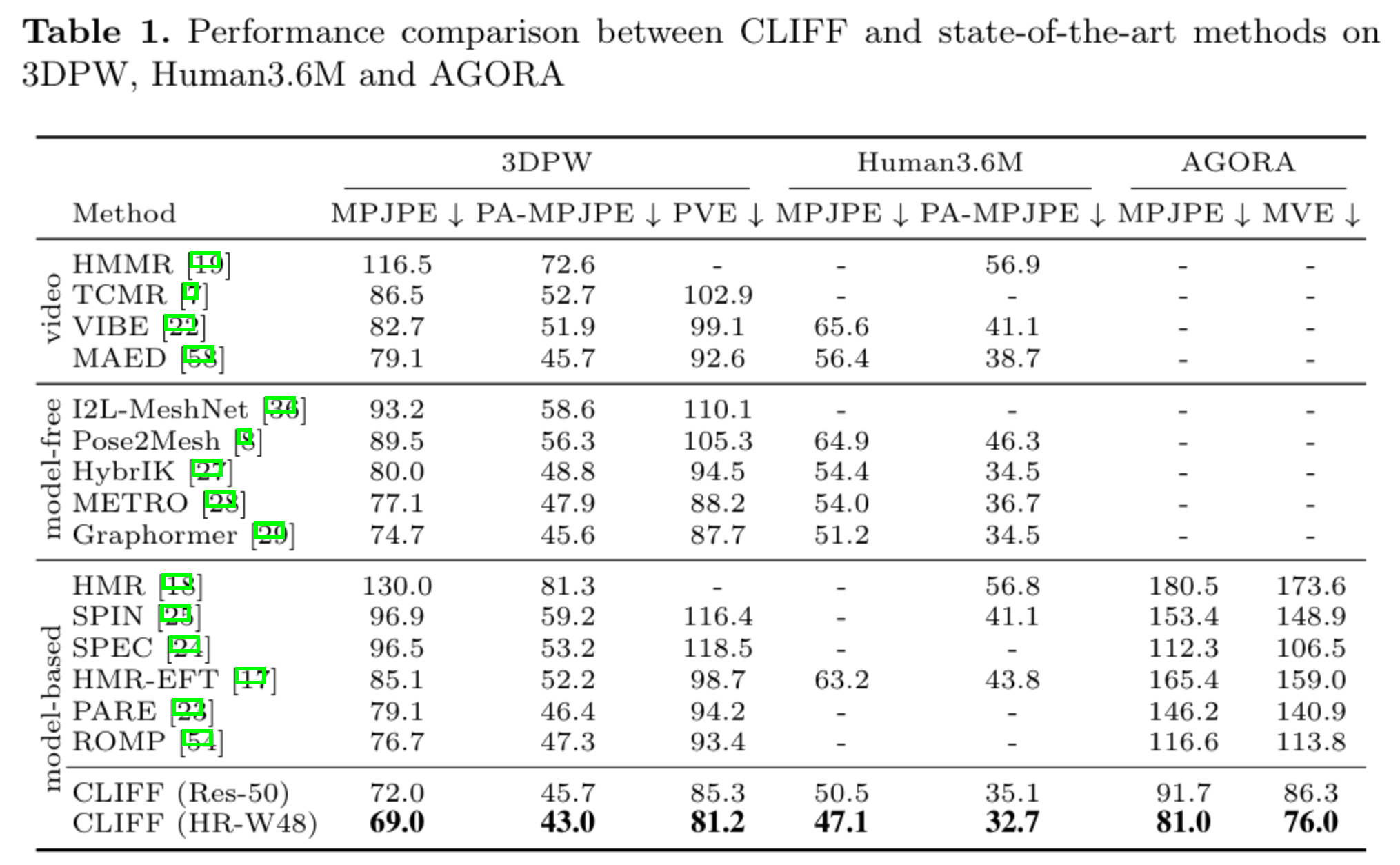
image.png

在多个数据集上多个指标上都获得了显著提升

消融实验

CI 代表 CLIFF Input 即是否将 bounding box 作为额外输入信息，CS 代表 CLIFF Supervision 代表是否在全图上计算 loss。 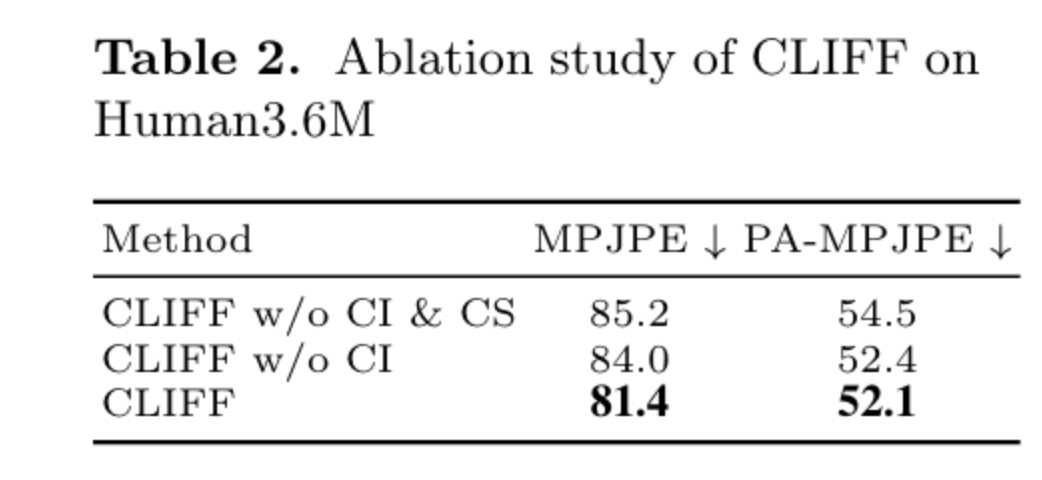image.png 从表 2 可以看到没有 CI 的话 MPJPE 指标变差很多，表明它对全局旋转估计有重要作用。同样，没有 CS 的话指标也有明显下降。 这个实验验证了作者全局信息对模型姿态估计的重要作用。

一些可视化结果 image.png