CornerNet: Detecting Objects as Paired Keypoints 链接到标题
* Authors: [[Hei Law]], [[Jia Deng]]
初读印象 链接到标题
CornerNet 预测目标的左上和右下角点heatmap, 提取焦点的 embedding 进行角点对匹配来替代 anchor
TL;DR 链接到标题
基于 anchor 的方法的缺点
- 需要铺设大量的 anchors,但是只有少量是和 gt 相交的有用 anchors, 带来了严重的正负样本不均匀问题;
- 引入大量的超参,
base_sizes、ratios、scales
为了解决上述问题提出 cornernet ,预测目标的左上和右下角点heatmap, 提取焦点的 embedding 进行角点对匹配来替代 anchor。
需要重点关注的有三个地方
- detecting corners
- grouping corners
- corner pooling
- hourglass network
Method 链接到标题
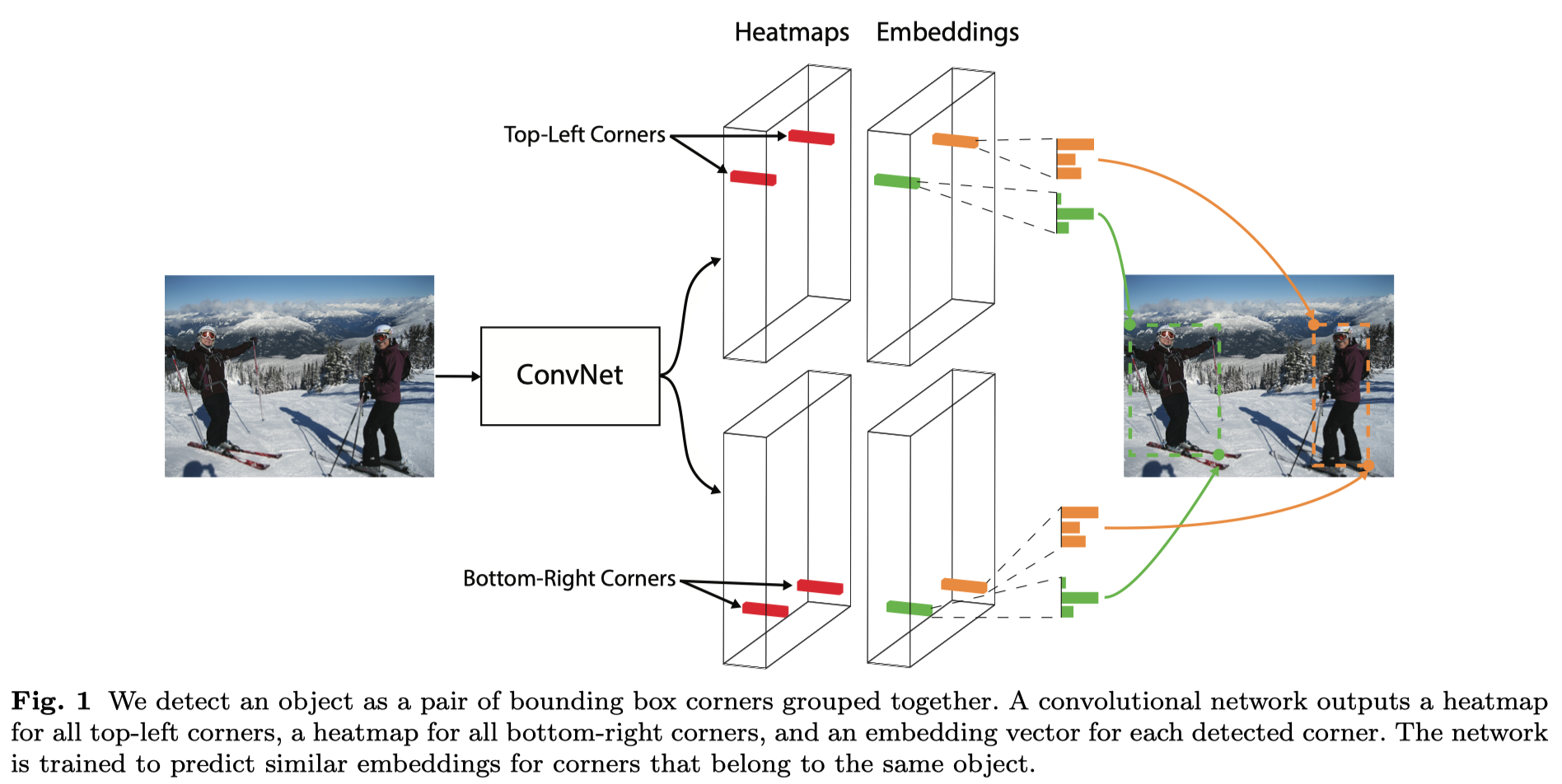 整体框架如上
整体框架如上
detecting corners 链接到标题
在 backbone 后面接两个 CxHxW 的分支, C 为目标类别数(注意不包括背景类别),每个点的值代表该点位对应类别目标一个角点的可能性。对于每一个角点存在一个 gt 位置,其他位置都是 negative。但是在训练的时候容忍 gt 周围 radius 范围的角点偏移误差,因为偏离了一点 gt 还是可能得到 iou 足够的预测框。 定位准确度用这个式子表示: $ e^{-\frac{x^{2}+y^{2}}{2 \sigma^{2}}} $ 其中 $\sigma=\frac{1}{3}radius$
基于此的角点 loss:
$$ L_{d e t}=\frac{-1}{N} \sum_{c=1}^{C} \sum_{i=1}^{H} \sum_{j=1}^{W}\left{\begin{array}{cc}\left(1-p_{c i j}\right)^{\alpha} \log \left(p_{c i j}\right) & \text { if } y_{c i j}=1 \ \left(1-y_{c i j}\right)^{\beta}\left(p_{c i j}\right)^{\alpha} \log \left(1-p_{c i j}\right) & \text { otherwise }\end{array}\right. $$
$p_{cij}$ 为位置 (i,j) 处, 类别 c 的分数。
由于 CNN 最后输出是经过下采样的,最后的坐标映射回原图会有损失,为此网络增加对映射误差的预测:
$$ \boldsymbol{o}{k}=\left(\frac{x{k}}{n}-\left\lfloor\frac{x_{k}}{n}\right\rfloor, \frac{y_{k}}{n}-\left\lfloor\frac{y_{k}}{n}\right\rfloor\right) $$
使用下面的 loss 来训练
$$ L_{o f f}=\frac{1}{N} \sum_{k=1}^{N} \operatorname{SmoothL} 1 \operatorname{Loss}\left(\boldsymbol{o}{k}, \hat{\boldsymbol{o}}{k}\right) $$
Grouping Corners 链接到标题
对于一张图有多个相同类别的目标的情形, 需要对预测的 corners 进行配对。 为每个预测的角点生成一个 embeding, 我们认为同一个目标的左上角和右下角 embeding 是近似的,所以通过比较 embeding 的距离可以确定哪些是配对的:
$$ \begin{array}{l}L_{\text {pull }}=\frac{1}{N} \sum_{k=1}^{N}\left[\left(e_{t_{k}}-e_{k}\right)^{2}+\left(e_{b_{k}}-e_{k}\right)^{2}\right] \ L_{\text {push }}=\frac{1}{N(N-1)} \sum_{k=1}^{N} \sum_{j=1 \atop j \neq k}^{N} \max \left(0, \Delta-\left|e_{k}-e_{j}\right|\right)\end{array} $$
$e_{tk}, e_{bk}, e_{k}$ 分别为左上角 embeding、右下角embedding, 左上右下embedding 的平均, $\Delta$ 设为 1。
Corner Pooling 链接到标题
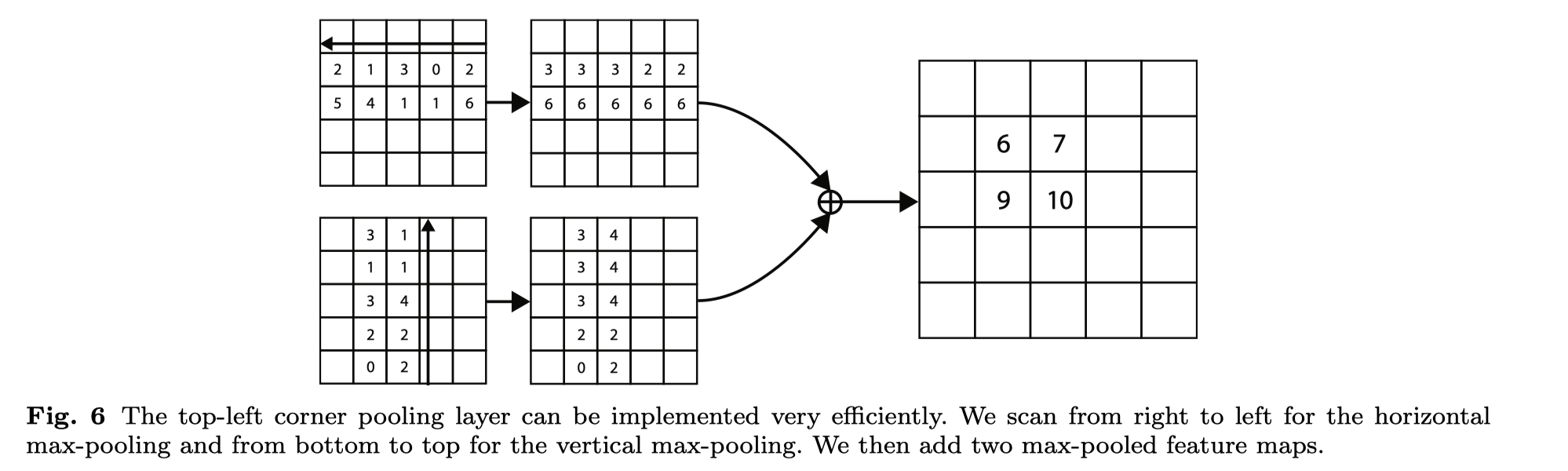
由于角点位置经常不包含目标,比如圆形目标检测框的角点周围都是背景信息, 为了确定上边界,需要从最左往最右看才能确定, 为了确定左边界,需要从上往下看才能确定。 作者提出了 Corner Pooling 的池化方法:
$$ \begin{array}{c}t_{i j}=\left{\begin{array}{cc}\max \left(f_{t_{i j}}, t_{(i+1) j}\right) & \text { if } i<H \ f_{t_{H j}} & \text { otherwise }\end{array}\right. \ l_{i j}=\left{\begin{array}{cl}\max \left(f_{l_{i j}}, l_{i(j+1)}\right) & \text { if } j<W \ f_{l_{i W}} & \text { otherwise }\end{array}\right.\end{array} $$

Hourglass Network 链接到标题
 总 loss:
总 loss:
$$ L=L_{d e t}+\alpha L_{p u l l}+\beta L_{p u s h}+\gamma L_{o f f} $$
Experiments 链接到标题

corner pooling 很重要,整体提升 2 个点,对大物体提升 3.6 个点

减小 gt 周围的惩罚对点数影响明显

Hourglass 很重要